Betrag
Mathematisch
|-15| = 15 heißt so viel wie: der Betrag der Zahl -15 ist 15. Und der Vektor (3|4|0) hat den Betrag 5: die gemeinsame Bedeutung ist die eines Abstandes, meist vom Nullpunkt einer Zahlengeraden oder eines Koordinatensystems. Lies mehr unter => Beträge
… etwas, das man bezahlt für eine bloße => Bereitstellung
Betrug
Definition
Ist im § 263 des deutschen Strafgesetzbuches klar definiert: wer in der Absicht, sich oder einem Dritten einen rechtswidrigen Vermögensvorteil zu verschaffen, das Vermögen eines anderen dadurch beschädigt, daß er durch Vorspiegelung falscher oder durch Entstellung oder Unterdrückung wahrer Tatsachen einen Irrtum erregt oder unterhält, wird mit Freiheitsstrafe bis zu fünf Jahren oder mit Geldstrafe bestraft. => Ganzen Artikel lesen …
Berg
Geographie
Definition: eine Geländeform, die deutlich höher als ihre unmittelbare Umgebung ist und mehr oder minder steile Hänge hat. Ein berühmter Berg ist zum Beispiel die Zugspitze in den deutschen Alpen. => Ganzen Artikel lesen …
Beträge
Begriffsklärung
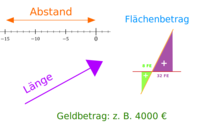
Beträge gibt es für Zahlen, Geldmengen, Vektoren, komplexe Zahlen, Integrale und andere mathematische Objekte. Die verschiedenen Bedeutungen werden hier kurz vorstellt. => Ganzen Artikel lesen …
Ertrag
Bedeutungen
In der Landschwirtschaft und im Kaufmannswesen: ein Ertrag in der Landwirtschaft ist eine Menge an geernteten Pflanzen, etwa Weizen oder Kartoffeln. Im Kaufmannswesen ist es eine Erhöhung des Gesamtvermögens. Beides ist hier kurz erklärt. => Ganzen Artikel lesen …
… de Absolutbetrag von -4 ist die Zahl 4, man sagt kurz nur => Betrag
Betrag als Geldwert
Geschäftswesen
Im Jahr 2021 verkündete der Unternehmer Elon Musk, dass er sein satellitengestütztes Internet „Starlink“ für einen monatlichen Betrag von 99 Euro für jedermann anbieten möchte. Das Wort Betrag steht hier für eine Geldmenge. Siehe auch => Betrag [als Wort an sich]
Betrag einer komplexen Zahl
Bedeutung | Schreibweise | Berechnung
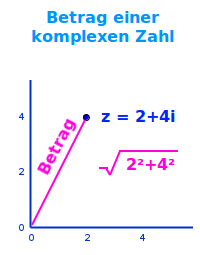
Der Betrag |z| einer komplexen Zahl z ist gleich ihrem Abstand vom Koordinatenursprung in der Gaußschen Zahlenebene. => Ganzen Artikel lesen …
Definition
|-4| = 4 - man liest: der Betrag von minus vier ist gleich vier. Der Betrag einer Zahl ist ihr Abstand von der 0, immer nur positiv genommen. Den Betrag einer Zahl gibt man mit je einem senkrechten Strichen links und rechts der Zahl an, den sogenannten Betragsstrichen. Das ist hier mit Beispielen weiter erklärt. => Ganzen Artikel lesen …
… der Vektor (4|0|0) hat den Betrag 4, der Betrag ist gleich der => Vektorlänge
Betragsfunktion
f(x) = |x|
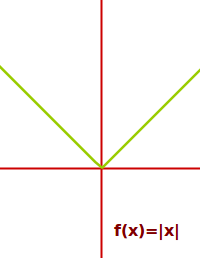
Die Betragsfunktion ordnet jedem x-Wert ihren Betrag zu. Der Graph besteht aus zwei Geraden, die sich im Punkt (0|0) treffen. Der linke Ast (mit negativen x-Werten) kann durch die Funktion f(x)=-x beschrieben werden. Der rechte Ast entspricht f(x)=x. Hier einige Beispielwerte: => Ganzen Artikel lesen …
Betragsfunktion ableiten
Wie man die erste Ableitung von f(x) = |x| bildet
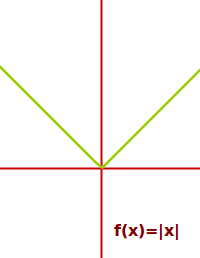
Der Graph der einfachen Betragsfunktion f(x)=|x| sieht aus wie der Buchtabe V. Die untere Spitze liegt im Punkt (0|0). Links davon ist die Steigung überall -1. Rechts davon ist Steigung überall +1, also 1. An der Stelle x=0 hat der Graph einen Knick und ist damit dort nicht differenzierbar (ableitbar). Die folgende Liste fasst diese Gegebenheiten zusammen: => Ganzen Artikel lesen …
Definition
Betragsgleich heißt, dass Zahlen gleich weit entfernt von der 0 sind: die Zahlen -4 und 4 sind betragsgleich: sie haben beiden den Abstand „4“ zur 0. Es wird kurz erklärt, was betragsgleich bei Zahlen, Vektoren und komplexen Zahlen bedeutet. => Ganzen Artikel lesen …
… ohne Vorzeichen wären es dieselben Zahlen, siehe auch => betragsgleich
wenn man Minus als Vorzeichen weglässt …
Bei Zahlen kann man ihr Vorzeichen und ihren Betrag unterscheiden. Das Vorzeichen sagt, ob sie auf dem Zahlenstrahl links oder rechts von der Null liegen. => Ganzen Artikel lesen …
Zahlen | Vektoren
Der Betrag einer Zahl ist ihr Abstand von der 0 auf der Zahlengeraden. Ein Betrag ist dabei immer positiv. Zwei senkrechte Striche links und rechts von einer Zahl oder einem Term bedeuten, dass der Wert des Termes immer positiv sein soll. => Ganzen Artikel lesen …
… die „normale“ Zinsformel => einfache Zinsformel
… das Geld, das man am Ende hat, z. B. im Kontext der => Zinsrechnung
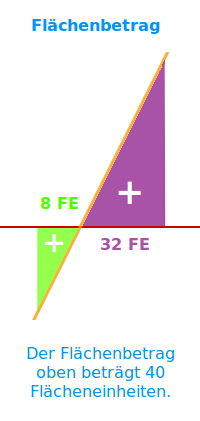Flächenbetrag
Alle Teilflächen sind +
In der Integralrechnung ist der Flächenbetrag die Summe aller positiv gerechneten Teilflächen, die ein Funktionsgraph mit der x-Achse bildet. Flächen unterhalb der x-Achse werden dabei auch positiv (+) gerechnet. Der Flächenbetrag kann nie negativ sein. Er ist entweder 0 oder eine positive Zahl. => Ganzen Artikel lesen …
Anleitung
Das Wort Flächenbetrag gehört in die Integralrechnung. Der Flächenbetrag meint hier den Flächeninhalt, den eine Kurve (z. B. eine Parabel) mit der x-Achse und zwei weiteren senkrechten Linien im Graphen einschließt. Hier steht eine kurze Anleitung zur Berechnung. => Ganzen Artikel lesen …
… die „normale“ Zinsformel => einfache Zinsformel
… siehe unter => Monatszinsen berechnen
1/(-4) hat 4
Der Bruch 1/(-4) hat als Nenner die Zahl -4. Der Betrag einer Zahl ist die Zahl ohne ein negatives Vorzeichen, hier also 4. Die Zahl 4 ist der Nennerbetrag der Bruch minus-ein-Viertel. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
Offener Betrag
… ... in der Kaufmannssprache: eine Rechnung, die noch nicht bezahlt ist, ein => Außenstand
… siehe unter => Tageszinsen berechnen
Vektorbetrag
Definition
Den Vektor (2|4|4) kann man sich als einen Pfeil vorstellen. Die Länge dieses Pfeiles nennt man auch Vektorlänge oder den Vektorbetrag. Man berechnet ihn, indem man alle einzelnen Koordinaten, also (2;4;4) quadriert (4;16;16), davon die Summe bildet (36) und von dieser Summe die Wurzel zieht: der Betrag des Vektors, also seine Länge, ist dann: 6 => Ganzen Artikel lesen …
Anleitung
√(x²+y²+z²) ist der Term zur Berechnung des Vektorbetrags: man rechnet jede einzelne Koordinate zum Quadrat, addiert diese Quadrate dann auf und zieht am Ende daraus die Wurzel. Das ist hier mit einem Beispiel erklärt. => Ganzen Artikel lesen …
… meint seine Länge, mehr unter => Vektorbetrag
… wenn man Vorzeichen nicht berücksichtigt, mehr unter => Betrag einer Zahl
Geometrie
Die Winkel -12° und 12° haben beide als Betrag den Wert 12. Der Betrag eines Winkels ist seine Größe ohne negative Vorzeichen geschrieben. Der Winkelbetrag gibt damit an, wie weit ein Winkel geöffnet ist, also wie groß er ist. Der Winkelbetrag gibt aber nicht an, in welche Richtung der Winkel geöffnet wurde oder zeigt. Interessant ist der Winkelbetrag etwa in der freiäugigen Astronomie als sogenannter => Sehwinkel
… siehe unter => Wochenzinsen berechnen
Brüche
Der Zählerbetrag von 3/4 ist die 3 und von (-3)/(4) wäre es auch die 3: die obere Zahl eines Bruches ist der Zähler. Sie immer als positive Zahl - also ohne Minuszeichen - ist dann der Zählerbetrag. Das ist hier weiter erklärt. => Ganzen Artikel lesen …
… |-3| ist 3, meint: ohne Vorzeichen, mehr unter => Betrag einer Zahl
… die Menge an Zinsen in Euros (oder Dollar), z. b. 48 €, weitere Fachworte unter => Zinsrechnung
