Betrag einer komplexen Zahl
Bedeutung | Schreibweise | Berechnung
© 2016
- 2025
Basiswissen|
Was meint der Betrag?|
Welche Schreibeweisen sind üblich?|
Wie berechnet man den Betrag?|
Synonyme
Basiswissen
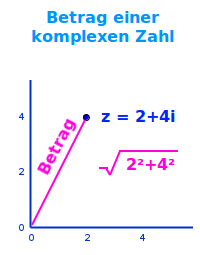
Der Betrag |z| einer komplexen Zahl z ist gleich ihrem Abstand vom Koordinatenursprung in der Gaußschen Zahlenebene.
Was meint der Betrag?
- Eine komplexe Zahl kann in der Gaußschen Zahlenebene veranschaulicht werden.
- Eine komplexe Zahl ist dort ein Punkt in einem Koordinatensystem.
- Der Betrag einer komplexen Zahl ist ihr Abstand zum Ursprung (0|0).
- Der Betrag einer komplexen Zahl ist immer eine reelle Zahl.
Welche Schreibeweisen sind üblich?
- |z| mit z als komplexe Zahl
- r als Bestandteil der Polarform r*e^(i*phi)
- r als Bestandteil der Exponentialdarstellung der Polarform r*[cos(phi)+isin(phi)]
Wie berechnet man den Betrag?
- In einer Polarform ist der Betrag unmittelbar über r gegeben.
- Aus der kartesischen Form (a+bi) kann er über Pythagoras berechnet werden:
- |z| = Wurzel aus [a²+b²]
- Alternativ gibt es noch den Weg über die konjugiert komplexe Zahl:
- z mal dem konjugiert Komplexen von z gibt auch den Betrag von z.