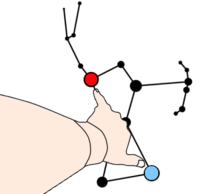
Winkelabstand
Astronomie
Basiswissen
Wie weit voneinander entfernt Sterne am Himmel erscheinen gibt man meist als Winkel an. Anschaulich gibt der Winkel an, wie weit man den Kopf drehen müsste, um von einem direkten Blick auf einen Stern auf einen anderen Stern zu schwenken.
Anschauliche Definition
Blickt man durch ein kleines Rohr auf einen Stern und dreht man dann den Kopf so, dass man durch das Rohr einen anderen Stern sieht, dann ist die Drehung des Kopfes in Winkelgrad angegeben der Winkelabstand zwischen den Sternen. Zwei Sterne, die sehr dicht beieinander liegen, haben zum Beispiel einen Winkelabstand von 2°. Typische Abstände von Sternen in Sternbildern sind 5° bis 20°.
Beispielhafte Winkelabstände von Sternen
◦ 27,1°: vom roten Riesen Beteigeuze zu unserem Nachbarn => Sirius
◦ 18,6°: vom roten Riesen Beteigeuze zum blauen Riesen => Rigel
◦ Diese Abstände entsprechen entwa einer großen => Handspanne
◦ Weitere Zahlenbeispiele stehen im Artikel => Winkelabstände
Wie kann man einen Winkelabstand schätzen?
Eine gute Schätzung der Winkelabstände liefert die Körperteil-Methode: man streckt einen Arm aus und macht dann zum Beispiel eine geballte Faust. Vom linken bis zum rechten Rand der Faust ist der Winkelabstand dann etwa 10°. Für eine große Spanne sind es zum Beispiel etwa 24° und der kleine Finger und Daumen liegen zwischen 1° und 2°. Große Sternbilder überdeckt man also in etwa mit der Faust oder einer Handspanne. Siehe dazu auch => Winkelschätzung
Wie kann man einen Winkelabstand messen?
Astrolabium, Jakobsstab, Dreistab, Theodolith und viele mehr: zur Messung eines Winkelabstandes gibt es sehr viele Geräte. Manche kann man leicht in der Hand halten (Astrolabium), andere müssen aufwändig aufgebaut werden (Dreibstab). Siehe mehr unter => Winkelmessung
Warum gibt man den Abstand nicht in Kilometern an?
Sterne oder Planeten, die am Himmel direkt nebeneinander erscheinen, können in Wirklichkeit sehr weit voneinander entfernt sein. Am 2. März 2023 zum Beispiel standen die Planeten Venus und Jupiter am Abendhimmel nur einen kleinen Fingerbreit voneinander am Abendhimmel. Ihr Winkelabstand lag unter 2° (sehr wenig). In Kilometern aber war Jupiter mit 741 Millionen Kilometern Abstand mehr als sieben mal so weit von uns entfernt wie die Venus mit nur 108 Millionen Kilometern Abstand. Würde man die Abstände der Himmelskörper in Kilometern zu uns oder auch in Kilometern zueinander angeben, würde das nicht zuverlässig sagen, wie weit entfernt sie uns am Himmel erscheinen. Der Abstand als Winkel in Grad passt sehr viel besser zu diesem scheinbaren Abstand. Für einen ähnlichen Effekt, siehe auch den Artikel => scheinbare Größe
Literatur
◦ [1] Wil Tirion, Storm Dunlop: Der Kosmos Sternenführer. Franckh-Kosmos Verlag, Stuttgart. 2004. ISBN: 3-440- 09785-4. Seite 92.
◦ https://stjerneskinn.com/angular-distance-between-stars.htm [entnommen am 7. März 2023]
