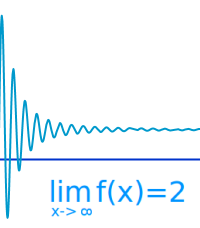
Unendlichkeitsverhalten
Analysis
Basiswissen
Was der y-Wert macht, wenn man mit x gegen unendlich geht: die Antwort auf diese Frage nennt man das Unendlichkeitsverhalten oder auch Globalverhalten einer Funktion. Man spricht auch von Grenzwerten für x gegen plus oder gegen minus unendlich. Typisch dafür ist die Schreibweise mit dem Limes. Das ist hier näher erklärt.
Wohin gehört das Stichwort?
- Das gehört zum Thema Funktionen und Graphen.
- Es ist ein Spezialfall von einem Grenzwert.
- Es geht um die Grenzwerte von x gegen plus oder minus unendlich.
- Siehe mehr zum Hintergrund unter => Grenzwert
Lösungsmöglichkeiten
Man unterscheidet drei Lösungsansätze: a) Zahlen einsetzen, b) den Graphen interpretieren und c) Grenzwerte rechnerisch bestimmen.
a) Zahlen einsetzen
Man setzt für x sehr große Zahlen (z. B. 999999999999999999999999) oder sehr kleine Zahlen (z. B. -99999999999999999999999999) ein. Man betrachtet, dann welchen Funktionswert f(x) oder y man erhält. Ist der Funktionswert dann zum Beispiel nahe an der Null, kann man vermuten, dass der Grenzwert wahrscheinlich 0 ist. Ist f(x) hingegen sehr groß, kann man vermuten, dass der Grenzwert selbst auch unendlich ist. Lies mehr dazu unter => Grenzwerte über Probieren
b) Den Graphen deuten
Hat man den Graphen einer Funktion, zum Beispiel mit Hilfe eines Taschenrechners, dann kann man für den Grenzwert f(x) gegen plus unendlich abschätzen, in welche Richtung der Funktionswert tendiert, wenn man auf der x-Achse immer weiter nach rechts geht. Ist der Grenzwert für f(x) gegen minus unendlich gesucht, versucht man abzuschätzen, in welche Richtung f(x) tendiert, wenn man auf der x-Achse immer weiter nach links geht. Für eine Übersicht zu Graphen siehe unter => Funktionsgraphen
c) Grenzwerte berechnen
Die Methoden a und b liefern oft gute Abschätzungen, aber niemals eine endgültige Sicherheit. Es gibt aber Rechenmethoden um Grenzwerte eindeutig und sicher zu bestimmen. Siehe als Beispiel die => Regel von l'Hospital
Was meint unendlich hier?
- Das meint, dass man für x immer größere oder immere kleinere Zahlen einsetzt.
- Immer größer wäre zum Beispiel: 1; 4; 6; 10; 100; eine Million; eine Trilliarde ...
- Immer kleiner wäre zum Beispiel: -1; -10; -100; minus eine Trilliarde etc.
- Immer größer spricht man aus: gegen plus unendlich.
- Immer kleiner spricht man aus: gegen minus unendlich.
- Siehe auch => Grenzwerte
Was meint Verhalten?
- Das Verhalten bezieht sich auf den y-Wert.
- Was macht er, wenn man mit x gegen plus oder minus unendlich geht?
- Im Beispiel f(x)=60:x wird y immer mehr zu 0, wenn man gegen plus unendlich geht.
- Man sagt: Für x gegen plus unendlich geht y gegen 0.
- Und für x gegen minus unendlich geht y auch gegen 0.
- Das ist das Unendlichkeitsverhalten.
- Siehe auch => Limes
