Basiswissen

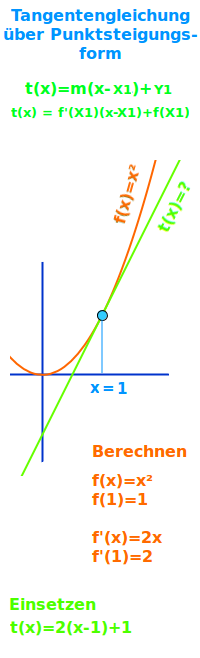
Gegeben ist eine Funktionsgleichung f(x) und der x-Wert eines Punktes (X1|Y1) auf dem Graphen. Daraus kann man die Gleichung t(x) in der Form t(x) = m·(x-X1)+Y1 der Tangente an dem Punkt (X1|X2) bestimmen. Dieser Rechenweg ist schnell ohne große Fehlermöglichkeiten. Das wird hier Schritt für Schritt erklärt.

Bildbeschreibung und Urheberrecht — Man sieht die Punksteigungsform einer Geradengleichung in zwei Varianten:☛

Kurzanleitung

Man setzt den gegeben x-Wert in f(x) ein und erhält damit die Zahlen des Punktes (X1|Y1) auf dem Graphen von f(x) als Zahlen. Diese Zahlen setzt man in die Punktsteigungsform t(x) =m(x-X1)+Y1 ein. Dann ist nur noch die Steigung m unbekannt. Diese bestimmt man über die erste Ableitung f'(x), indem man dort den gegebenen x-Wert einsetzt einsetzt.

Ausführlich

Als Beispiel betrachtet wird die Funktion: f(x)=x²

Gesucht ist die Tangentengleichung t(x) an der Stelle: x=1

Dazu muss man als Zahlen bestimmen: X1, Y1 und m

X1 bestimmen

X1 ist gleich dem gegebenen x-Wert:

Im Beispiel also: X1 = 1 ✔

Y1 bestimmen

Man setzt X1 ein in f(x):

Im Beispiel: f(1) = 1²

Also: Y1 = 1 ✔

m bestimmen

Die Funktion f(x) einmal ableiten:

Das gibt im Beispiel: f'(x) = 2x

Den X1-Wert dort einsetzen.

f'(1) = 2·1 = 2

Also: m = 2 ✔

t(x) aufstellen

Die Punktsteigungsform lautet: t(x) = m(x-X1)+Y1

Die oben bestimmten Zahlenwerte einsetzen:

Die Tangentengleichung ist: t(x) = 2·(x-1)-1

Vereinfachen: t(x) = 2x-3 ✔

Gibt es noch andere Verfahren?

Das Verfahren hier ist in der Schulmathematik eher unüblich.

Andere Verfahren stehen unter Tangentengleichung aufstellen ↗

qck
qck