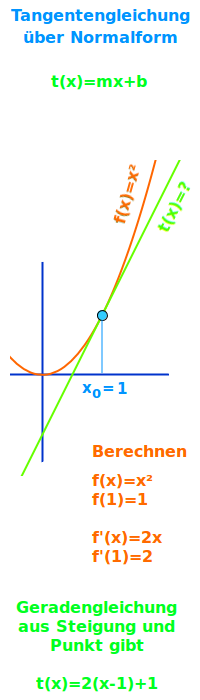
Tangentengleichung über Normalform

Wie man t(x)=mx+b für eine Tangente findet

Basiswissen

Aufabentyp

• Gegeben ist die Funktion, z. B.: f(x)=x².
  

• Gegeben ist ist eine Stelle xo (sprich: x-Null), im Beispiel xo=1.
  

• Auf dem Graphen von f(x) gibt es einen Punkt mit diesem x-Wert.
  

• An diesen Punkt soll eine Tangente angelegt werden.
  

• Eine Tangente ist immer eine Gerade.
  

• Gesucht ist ihre Gleichung in Normalform.
  

I. Normalform aufschreiben

• Schreibe die Normalform hin: t(x)=mx+b.
  

• (Oft findet man statt f(x) auch y, also: y=mx+b)
  

• Ziel ist es, für m und b Zahlen zu bestimmen.
  

• Das m ist die Steigung der Tangente.
  

• Das b ist ihr y-Achsenabschnitt.
  

• Siehe auch y=mx+b ↗
  

II. Berührpunkt bestimmen

• Dort wo die Tangente den Graphen von f(x) berührt ...
  

• dort haben f(x) und die Tangente dieselben x- und y-Werte.
  

• Dieser gemeinsame Punkt von f(x) und t(x) heißt auch Berührpunkt ↗
  

• Der x-Wert, manchmal auch Stelle genannt, ist meistens gegeben.
  

• Wenn man den gegeben x-Wert (hier 1) in f(x) einsetzt, ...
  

• dann hat man automatisch den y-Wert von f(x) und ...
  

• damit auch von der Tangente, im Beispiel: f(1)=1
  

• Also hier im Beispiel (1|1) der Berührpunkt ↗
  

• Der Berührpunkt ist auch ein Punkt der gesuchten Tangente.
  

• Was noch fehlt ist die Steigung der Tangente.
  

• Diese wird im nächsten Schritt berechnet.
  

III. Steigung m bestimmen

• Dort wo x=1 ist berührt die Tangente den Graph von f(x).
  

• Das Berühren meint automatisch auch, dass, ...
  

• f(x) und t(x) an dem Berührpunkt dieselbe Steigung haben.
  

• Von f(x) kann man die Steigung über die erste Ableitung finden.
  

• Man leitet f(x) dann ab zu f'(x) und setzt den ...
  

• in der Aufgabenstellung vorgegebenen x-Wert ein.
  

• Im Beispiel: f'(x)=2x, dafür x=1 einsetzen gibt: 2
  

• Die Steigung m der Tangente ist dann m=2.
  

• Jetzt kennt man die Steigung der Tangente.
  

• Und man kennt einen Punkt der Tangente (Schritt II)
  

• Damit kann man im nächsten Schritt die Geradengleichung aufstellen.
  

IV Geradengleichung aufstellen

• Jetzt hat man die Steigung und einen Punkt einer Geraden.
  

• Wie man daraus zu einer Geradengleichung (mit b) kommt ist ...
  

• erklärt unter Geradengleichung aus Steigung und Punkt ↗
  

V Ergebnis aufschreiben

• Im Beispiel wäre das Ergebnis t(x)=2(x-1)+1
  

• Vereinfacht gibt das: t(x)=2x-1 ✔