A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 9 Ω
Das Banner der Rhetos-Website: zwei griechische Denker betrachten ein physikalisches Universum um sie herum.

Pythagoreisches Tripel

Dreiecke

© 2016 - 2025


Basiswissen｜ Was meint pythagoreisch?｜ Was ist ein Tripel?｜ Was ist ein pythagoreisches Tripel?｜ Was wäre ein Beispiel?｜ Bildungsformeln｜ Was ist der Satz von Fermat?｜ Fußnoten


Basiswissen


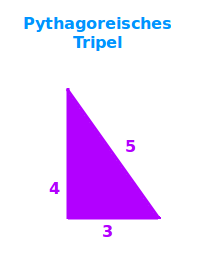
3, 4 und 5: wenn das die Längen der Seiten ein und desselben Dreiecks sind, dann heißen die Zahlen pythagoreisches[1] Tripel: drei natürliche Zahlen, die als Dreieckslängen exakt auf ein rechtwinkliges Dreieck passen nennt man pythagoreische Tripel. Es gibt unendlich viele solche Tripel.



Bildbeschreibung und Urheberrecht
Drei Zahlen, die eingesetzt auf den Satz des Pythagoras passen, nennt man ein pythagoreisches Tripel☛


Was meint pythagoreisch?


  • Das meint, dass es um rechtwinklige Dreiecke geht.
  • Das sind Dreiecke mit genau einem 90-Grad-Winkel.

Was ist ein Tripel?


  • Das Wort "Tripel" meint immer: drei Dinge.
  • Hier meint Tripel: drei natürliche Zahlen.
  • Ein solches Tripel wäre etwas 3; 4 und 5.

Was ist ein pythagoreisches Tripel?


  • Das sind drei natürliche Zahlen, die als Seitenlängen genau auf ein rechtwinkliges Dreieck passen.
  • Sie passen dann auch immer auf die Gleichung: a² + b² = c²

Was wäre ein Beispiel?


  • Wenn die Seitenlängen eines Dreiecks genau ...
  • 3; 4 und 5 cm sind, dann ist das Dreieck rechtwinklig.
  • Das gleiche passt auf die Zahlen 5; 12 und 13.
  • Probe: 5² + 12² = 13² geht exakt auf, passt also.

Bildungsformeln


Es gibt drei einfache Bildungs- oder Erzeugungsformeln für pythagoreische Tripel:

  • a = m²-²
  • b = 2·m·n
  • c =m²+m²

Diese drei Formeln geben für beliebige natürliche Zahlen n und m ein Pythagoreischen Tripel, wenn gilt: m > n > 0.

Was ist der Satz von Fermat?


  • für a² + b² = c² gibt es unendlich viele pythagorerische Tripel.
  • Gilt das auch für a³ + b³ = c³? Das war über Jahrhundert unklar.

Fußnoten


  • [1] Dem Deutschen Wörterbuch der Deutschen Sprache (DWDS) zufolge (Stand 2024) ist pythagoreisch das korrektive Adjektiv zu Pythagoras. In: der Artikel "pythagoreisch". Siehe zum Beispiel pythagoreischer Aufzug ↗
  • [2] Die drei Bildungsformeln wurden schon wurden schon von Euklid angegeben (Elemente, Buch 10, Proposition 29, Lemma 1). Siehe auch Euklid ↗