Basiswissen

Man nennt einen Graphen aus Knoten (Ecken) und Kanten dann planar, wenn man ihn in einer Ebene so darstellen kann, dass sich keine der Kanten gegenseitig kreuzen.^[1] Mit planaren Graphen können bereits Grundschüler tiefsinnige mathematische Betrachtungen durchführen.^[2]

Bildbeschreibung und Urheberrecht — Jeden Menge von Knoten (Punkten), gegebenenfalls kreuzungsfrei verbunden durch Kanten (Linien) ist ein planarer Graph. Kanten dürfen zurück zu ihrem Ausgangspunkt führen (Schleifen bilden) oder auch zwischen denselben zwei Punkten verlaufen (benachbarte Kante). Nicht erlaub sind Kreuzungen von Kanten und Kanten, die nicht genau zwei Punkte verbinden.☛

Definition

Ein Graph im Sinne der Graphentheorie (um die es hier geht) ist ein Diagramm, das nur aus sogenannten Knoten und anten besteht. Die Knoten und Kanten können, müssen aber nicht, in einer 2D-Ebene liegen. Sie können auch in einem dreidimensionalen Raum angeordnete sein. So kann man auch einen Würfel als Graph auffassen, wenn man ihn auf seine 8 Ecken als Knoten und seine 12 Kanten beschränkt.

DEFINITION:

Ein Graph heißt planar, wenn man ihn in einer Ebene so darstellen kann, dass sich keine der Kanten kreuzen.

Mit dieser Definition wird es möglich sein, dreidimensionale Graphen, etwa die Ecken und Kanten einer Pyramide, auch zweidimensional auf eine Blatt Papier darzustellen.

Kanten

Eine Kante muss per Definition immer genau zwei Knoten verbinden.

Ein Strich, der in einem Knoten beginnt aber dann nicht in einem anderen Knoten endet, gilt nicht als Kante im Sinne der Graphentheorie.

Ob die Kanten als gerade Strecke, als geschwungene Linie oder als als gezacketer Strich gezeichnet sind, ist dabei unwichtig. Kanten dürfen, solange sie zwei Knoten verbinden, jede beliebige Linienform haben.

Eine Kante darf auch in demselben Knoten enden, an dem sie gestartet ist. Eine solche Kante heißt dann Schleife.

Es dürfen zwischen zwei Knoten auch mehrere Kanten gezeichnet werden. Diese nennt man dann Mehrfach- oder Multikanten.

K oder k^[1] ist eine übliche Abkürzung für die Anzahl von Kanten in einem Graphen.

Knoten

Knoten stellt man sich am besten als Punkte vor.

Der einfachste planare Graph besteht aus nur einem Knoten ohne Kanten. Das ist dann einfach ein Punkt in einer Ebene oder im Raum.

Denkt man sich einen zweiten Knoten an einem anderen Ort hinzu, kann man diese durch eine einzige Kante verbinden. Das ist der einfachst mögliche Graph.

Zwei Knoten, die durch eine Kante verbunden sind, heißen benachbart.

E oder e^[1] ist eine übliche Abkürzung für die Knoten (Ecken) in einem Graphen.

Flächen

Im 3D-Raum zählt man als Flächen nur solche, die von Kanten umschlossen sind. Stellt man sich einen Würfel als Graphen vor, dann hat er genau 6 Flächen. Eine Dreieckspyramide hat genau vier Flächen.

In 2D-Flächen zählt man als Flächen, auch Facetten oder Gebiete genannte, alle Flächen die a) von Kanten umgeben sind, wie auch b) die alles umgebende äußere Fläche. Ein Dreick ist dann ein Graph mit E=3 Knoten, K=3 Kanten und F=2 Flächen.

F oder f^[1] ist eine übliche Abkürzung für die Anzahl von Flächen in einem Graphen.

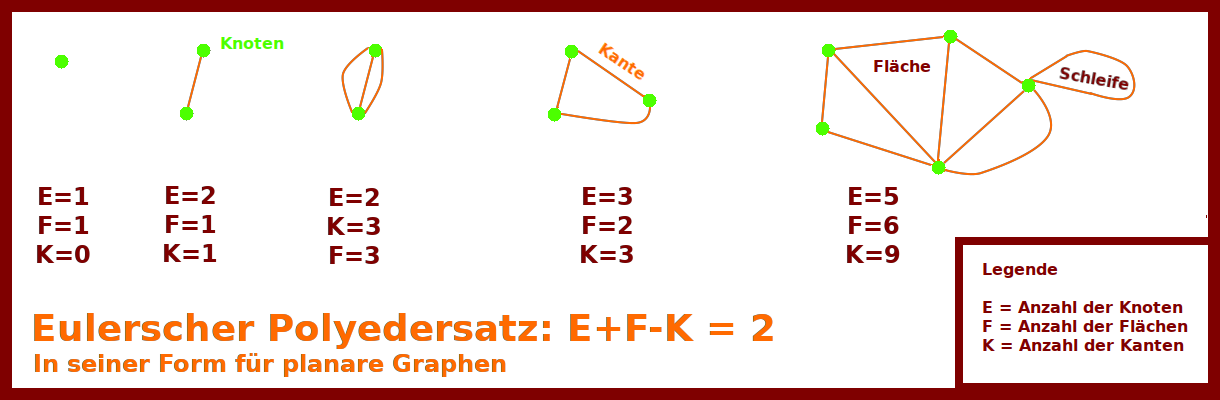
Eulerscher Polyedersatz

Der Eulersche Polyedersatz, benannt nach dem schweizer Mathematiker Leonhard Euler (1707 bis 1783), besagt, dass die Summe aus der Anzahl E der Knoten und der Anzahl F der Flächen vermindert um die Anzahl der Kanten K immer die Zahl 2 ergibt:

E+F-K = 2

Polyeder

Tatsächlich ist ein Polyeder ein dreidimensionaler Körper und keine flache Figur. Typische Polyeder sind zum Beispiel ein Würfel, eine Pyramide oder ein Tetrader. Ein Polyeder im Sinne der Geometrie hat immer Ecken und zwischen den Ecken verlaufen immer gerade Kanten. Und zischen denselben zwei Ecken kann es nur genau eine Kante geben. Eine äußere Begrenzungsfläche eines Polyeders (Vielflächner) ist damit auch immer ein 👉 Polygon [Vieleck]

In der Graphentheorie wird das anders betrachtet: zuerst bezeichnet man die Ecken jetzt als Knoten. Und die Kanten müssen nicht gerade sein. Und es darf auch mehrere Kanten zwischen denselben zwei Knoten geben.

Ecken in der Geometrie sind Knoten in der Graphentheorie.

Kanten in der Geometrie müssen gerade sein, nicht aber in der Graphentheorie.

Nur eine Kante zwischen zwei Ecken der Geometrie, aber Nachbarkanten sind erlaubt in der Graphentheorie.

Abstraktion

Wesentlich für die Graphentheorie ist alleine, welche Knoten mit wie vielen Kanten zu welchen anderen Knoten verbunden sind. Man streift also vom ursprünglichen geometrischen 3D-Körper als unwesentlich ab, die genaue Form und Lage der Ecken und Kanten. Diese Abstreifen nennt man auch abstrahieren. Und so kann man die Beziehungen zwischen Ecken und Kanten eines geoemtrischen Polyeders letztendlich ohne Informationsverlust auch zweidimensional als planaren Graphen darstellen. Der 2D-Graph ist dann eine Abstraktion des 3D-Körpers. Historisch wurde das Gesetz E+F-K =2 als echten Polyedern formuliert. Siehe dazu den Artikel 👉 Eulerscher Polyedersatz

Fußnoten

[1] Ein "planarer Graph" ist ein "plättbarer Graph, ein Graph, der eine kreuzungsfreie Einbettung G′ […] in die Ebene ℝ² besitzt. Die Einbettung G′ heißt ebener Graph." In: Guido Walz: Spektrum Lexikon der Mathematik. Band 4: Moo bis Sch; 2002; ISBN: 3-8274-0436-3. Dort der Artikel "Planarer Graph".

[2] Eine ausführliche Beschreibung eines Workshops mit acht Jahre alten Grundschülerinnen zum Eulerschen Polyedersatz findet man in: Joel David Hamkins: Math for eight-year-olds: graph theory for kids! 6. April 2015. Online: https://jdh.hamkins.org/math-for-eight-year-olds/