Parabelgleichung
Definition
© 2016
- 2026
Basiswissen
Der Graph einer quadratischen Funktion ist immer eine Parabel. Die Funktionsgleichung ist damit immer auch eine Parabelgleichung. Aber nicht jede Parabel in einem xy-Koordinatensystem kann als quadratische Funktion geschrieben werden. Das ist hier kurz erläutert.
Parabelgleichung als Funktion
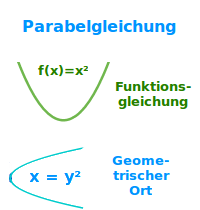
Eine Gleichung ist nur dann eine Funktionsgleichung, wenn es im Funktionsgraphen keine zwei Punkte gibt, die senkrecht übereinander liegen. Mit anderen Worten: es darf keine zwei Punkte oder Wertepaare mit demselben y-Wert geben. Kann das ausgeschlossen werden und ist der Graph eine Parabel, dann handelt es sich um eine Funktionsgleichung. Jede Gleichung, die man in die Form f(x) = ax²+bx+c bringen hat als Graph eine Parabel und ist eine Funktion, genauer gesagt, eine 👉 quadratische Funktion
Parabelgleichung nicht als Funktion
Weist der Graph einer Gleichung zwei Punkte auf, die senkrecht übereinander liegen, dann liegt keine Funktion vor. Es handelt sich dann allgemein zwar noch um eine Zuordnung, aber keine Funktion mehr. Das ist zum Beispiel der Fall, wenn die Parabel in einem xy-Koordinatensystem nach links oder rechts gekippt ist oder sogar waagrecht liegt. Man kann immer noch eine Gleichung für die Parabel aufstellen, sie ist aber keine Funktionsgleichung. Lies mehr dazu unter 👉 Parabel als geometrischer Ort