Nullstellen von gemischtquadratischen Funktionen bestimmen
Beispiel
© 2017
- 2025
Basiswissen
Wenn in einer quadratischen Funktion sowohl ein Term mit x² wie auch ein Term mit x vorkommt, dann nennt man diese Funktion gemischtquadratisch. Die allgemeine Form ist f(x) = Ax² + Bx + C. Hier stehen Methoden zur Berechnung der Nullstellen.
Kurzinfo
- Allgemein: f(x) = Ax² + Bx + C
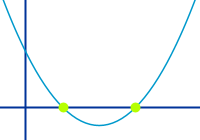
- Beispiel: f(x) = 0,5x² - 2x + 1,5
- Mit A = 0,5; B = -2 und C = 1,5
Legende
- f(x) = Funktionswert, wird oft auch y genannt.
- A = eine beliebige (außer Null) konstante Zahl, die aber fest vorgegeben ist
- B = eine beliebige (außer erlaubt) konstante Zahl, die aber fest vorgegeben ist
- C = eine beliebige (Null ist erlaubt) konstante Zahl, die fest vorgegeben ist
pq-Formel
- Die pq-Formel funktioniert immer.
- Immer erst f(x) Null setzen.
- Wäre hier: 0 = 0,5x² - 2x + 1,5
- Wenn A ungleich 1 ist, erst beide Seiten durch A teilen.
- Das gibt: 0 = x² - 4x + 3
- Die -4 ist jetzt das p.
- Die +3 ist jetzt das q.
- Siehe dann 👉 pq-Formel
Umformen
- Geht hier nicht, man kriegt x-quadrat und x nicht getrennt
- Besser: Probieren, pq-Formel oder ABC-Formel
ABC-Formel
- Geht immer
- Das A aus der Formel wäre das A aus der Funktionsgleichung oben.
- Das B aus der Formel wäre das B aus der Funktionsgleichung oben.
- Das C aus der Formel wäre das C aus der Funktionsgleichung oben.
- Damit jetzt die ABC-Formel rechnen
- Lösung: x=1 und x=3
- Siehe auch 👉 ABC-Formel
Faktorisieren
- Faktorisieren meint hier dasselbe wie Ausklammern.
- Ein Glied ohne x heißt ein absolutes Glied.
- Beispiel: f(x)=4x²+2x+5 ⭢ 5 ist absolutes Glied.
- Gibt es kein absolutes Glied, dann kann man gut faktorisieren.
- Beispiel: f(x)=4x²+2x wird zu f(x)=2x·(x+1)
- Daraus liest man leicht die Nullstellen ab: 0 und -1.