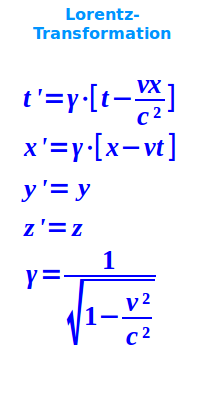Lorentz-Transformation

Physik

Basiswissen｜ Die Grundidee der Lorentz-Transformation｜ Die Formeln der Lorentz-Transformation｜ Legende｜ Voraussetzungen für die Lorentz-Transformation｜ Zum Sinn der Lorentz-Transformation｜ Quaestiones｜ Fußnoten

Basiswissen

Die sogenannte Lorentz-Transformation ist der mathematische Ausgangspunkt von Albert Einsteins spezieller Relativitätstheorie aus dem Jahr 1905. Die dazugehörigen Formeln gehen nicht über die Mathematik der Realschule hinaus^[1]. Aus dieser Transformation ergeben sich dann weitere Effekte der Relativitätstheorie wie etwa die Längenkontraktion^[2] oder die Zeitdilatation^[3].

Bildbeschreibung und Urheberrecht — Wie rechnet man die räumlichen und zeitlichen Koordinaten von einem Koordinatensystem in ein anderes herüber, wenn sie die Systeme zueinander bewegen und die Lichtgeschwindigkeit konstant sein soll?☛

Die Grundidee der Lorentz-Transformation

Angenommen man hat zwei verschiedene Koordinatensysteme S und S'. Man liest das als S und S-Strich. Die zwei Koordinatensysteme bewegen sich dabei a) mit einer gleichbleibenden, konstanten Geschwindigkeit b) die Bewegung zueinander erfolgt entlang einer geraden Linie und c) die Ursprünge der Koordinatensysteme lagen zum Zeitpunkt 0 beide an derselben Stelle.

MERKSATZ:

1.0 Mit der Lorentz-Transformation kann man Koordinaten aus einem System S in die Koordinaten eines Systems S' umrechnen.

Wenn diese drei Voraussetzungen erfüllt sind, dann kann man die Koordinaten eines Ereignisses aus dem System S in die Koordinaten des gestrichenen Systems S' umrechnen. Ein Ereignis ist dabei irgendetwas, das man über die Raumkoordinaten und die Zeitkoordinaten genau festlegen kann.

Die Formeln der Lorentz-Transformation

t' = γ·[t - vx/(c²)]

x' = γ·(x-vt)

y' = y

z' = z

Legende

t' = Zeitkoordinaten des Beobachters in S'

x' = x-Koordinate des Beobachters in S'

y' = y-Koordinate des Beobachters in S'

z' = z-Koordinaten des Beobachters in S'

t = Zeitkoordinaten des Beobachters in S

x = x-Koordinate des Beobachters in S

y = y-Koordinate des Beobachters in S

z = z-Koordinaten des Beobachters in S

γ = griechisches Gamma für den Lorentzfaktor ↗

γ = 1/[Wurzel aus (1-(v/c)²)]

· = Malzeichen für die Multiplikation

v = Geschwindigkeit des Inertialsystem S' relativ zu S

c = Lichtgeschwindigkeit = 300000000 m/s

Voraussetzungen für die Lorentz-Transformation

S und S' sind Intertialsysteme.

S und S' bewegen sich gleichförmig und geradlinig zueinander.

Die ungestrichenen Größen sind die Koordinaten von S.

Die gestrichenen Größen sind die Koordinaten von S'.

Zum Zeitpunkt t=0 muss auch t'=0 gewesen sein.

Bei t=t'=0 muss auch gelten: x=x', y=y' und z=z'.

S' bewegt sich geradlinig in positiver x-Richtung von S.

Die Relativgeschwindigkeit von S' zu S ist v.

Bewegt sich S' in negativer x-Richtung von S, wird v negativ eingesetzt.

Zum Sinn der Lorentz-Transformation

Die Grundidee der Lorentz-Transformation ist es, die Koordinaten eines Ereignisses von einem Koordinatensystem in ein anderes umzurechnen. Dabei sind die zwei Koordinatensysteme nicht starr zueinander ruhend^[4], sondern geradlnig und mit konstanter Geschwindigkeit zueinander bewegt^[5].

MERKSATZ:

2.0 Bei der Lorentz-Transformation geht es nur um die Umrechnung von Koordinaten von einem in ein anderes Koordinatensystem.

Angenommen ein Koordinatensystem von einer Flugüberwachung habe seinen Nullpunkt im Tower^[6]. Das Koordinatensystem eines Flugzeuges hingegen habe seinen Nullpunkt im Cockpit. Dieses Flugzeug soll geradeaus mit konstanter Geschwindigkeit in Richtung Flughafen fliegen. Nun kann man die Koordinaten des Anfangs der angesteuerten Landebahn in beiden Koordinatensystemen angeben. Während diese Koordinaten für das System im Tower ständig gleich sind, würde sie sich aber für das anfliegende Flugzeug ständig verändern. Kennt man die Koordinaten im Tower-System, und kennt man gleichzeitig auch die Geschwindigkeit und Flugrichtung des Flugzeug-Systems, dann kann man die Koordinaten von einem ins andere System umrechnen.

MERKSATZ:

3.0 Die Lorentz-Transformation gilt für Koordinatensysteme, die sich geradlinig und mit gleichbleibender Geschwindigkeit zueinander bewegen und deren Ursprünge zum Zeitpunkt 0 beider Systeme an derselben Stelle lagen.

Das Wesentliche an der Lorentz-Transformation ist der Faktor γ, ein kleines Gamma, auch Lorentzfaktor genannt. Er wird mit einer eigenen kleinen Formel aus der Relativgeschwindigkeit v berechnet^[7]. In diesem Faktor stecken die sogenannten relativistischen Effekte von Einsteins Theorie. Der Faktor bewirkt, dass wischen denselben zwei Ereignissen im System S zum Beispiel 2 Sekunden Zeitdauer liegen, während im System S' 10 Sekunden zwischen den Ereignissen vergehen. Der Zeitunterschied ist keine Frage der bloßen Wahrnehmung sondern real. Nicht wie wir Raum und Zeit wahrnehmend, sondern wie Raum und Zeit sind, ist relativ.

MERKSATZ:

4.0 Das rechnerische "Maschinenhaus" der Lorentz-Transformation ist der Faktor γ, sprich Gamma.

Aber, so könnte man einwenden, wenn man auf einem Schiff an einer Küste entlang schippert, dann ist doch Zeit zwischen der Abfahrt und er Ankunft am Zielhafen für das Schiff dieselbe wie für den Zielhaften am Festland. Nein, ist sie nicht. Sehr genaue Uhren können tatsächlich einen Zeitunterschied messen. Wir merken im Alltag davon nur nichts, weil der Unterschied so klein ist. Ein Schiff hat eine eher kleine Relativgeschwindigkeit^[8] zum Festland. Erst wenn die Relativgeschwindigkeit relativ hoch ist, muss man mit der Lorentz-Transformation rechnen, ansonsten nutzt man die viel einfachere Galilei-Transformation^[9]. Meist^[10] erst bei hohen Geschwindigkeiten rechnet man relativistisch ↗

MERKSATZ:

5.0 Wichtig für die Stärke der Effekte sind hohe Relativgeschwindigkeiten.

Ein letzter Gedanke soll die Entstehungsgeschichte der Relativitätstheorie betrachten. Bis ins späte 19te Jahrhundert hatte man für Umrechnungen von einem in ein anderes Koordinatensystem oft die sehr viel einfachere Galilei-Transformation benutzt. Dabei hat man keine Fehler entdecken können. Ein verblüffender Fehler trat erst auf, als man die Lichtgeschwindigkeit im Bezug zur Bahngeschwindigkeit der Erde messen wollte^[11]. Das verblüffende an dem Experiment - und das wofür die Lorentz-Transformation überhaupt erst nötig wurde - war die sogenannte Konstanz der Lichtgeschwindigkeit ↗

Quaestiones

1) Definiert man als Ereignis, dass das hintere Ende und die vordere Spitze eines langen Raumschiffes in einem Koordinatensystem S zu einem Zeitpunkt t=0 Lampen an den x-Positionen x=10 und x=20 sind, so wird die Transformation in ein relativ zu S bewegtes Koordinatensystem S' ergeben, dass die Ereignisse dort in S' zu verschiedenen Zeitpunkten auftreten. Wie soll man das hinsichtlich der der Identität des Raumschiffes deuten? Offensichtlich gilt nicht mehr der Spruch, dass ein Objekt aus Einzelteilen besteht, die zu einem bestimmten Zeitpunkt fest zusammengehören. Wenn sich die zwei betrachteten Punkte langsam über die ändern, zum Beispiel verrosten, dann könnte es sein, dass im Koordinatensystem S beide Enden immer im gleichen Zustand der Verrostung sind, im Koordinatensystem S' allerdings könnte es sein, dass der eine Punkt schon wesentlich rostiger ist als der andere. Welche Folgerungen müsste man daraus für die Idee einer Identität des Raumschiffes ziehen. Müsste man nicht davon ausgehen, dass es dann auch zwei verschiedene Raumschiffe gibt, nämlich ein gleichmäßig rostendes und ein ungleichmäßig rostendes?

Fußnoten

[1] Albert Einstein hat die Herleitung und Deutung der Lorentz-Transformation selbst in klarer und fast mathematikfreier Sprache selbst in einem kleinen Buch erklärt: Über die spezielle und allgemeine Relativitätstheorie. Ersterscheinung: 1916.

[2] Als Längenkontraktion bezeichnet man den Effekt, dass die Länge eines Gegenstandes tatsächlich kleiner wird, wenn man es von einem (relativ zum Gegenstand) bewegten Koordinatensystem aus sieht. Siehe auch Längenkontraktion ↗

[3] Als Zeitdilatation bezeichnet man den Effekt, dass die Zeitdauer zwischen zwei Ereignissen länger wird, wenn man die Ereignisse von einem (relativ zu den Ereignissen) bewegten Koordindatensystem aus betrachtet. Siehe auch Zeitdilatation ↗

[4] Starr zueinander ruhend wären zum Beispiel zwei Koordinatensysteme mit Längen- und Breitengraden für die Oberfläche der Erde. Das eine Koordinatensystem könnte seinen nullten Längengrad durch London gehen lassen, das andere durch Paris. Durch einfache Additionen und Subtraktion kann man dann die Koordinaten einer Insel umrechnen. Siehe mehr dazu unter Galilei-Transformation ↗

[5] Zwei Koordinatensysteme können sich relativ zueinander zum Beispiel mit wechselnden Geschwindigkeiten und in Schlangenlinien bewegen. Erfolgt die Bewegung aber nur geradlinig und mit ständig gleicher, das heißt konstanter Geschwindigkeit, dann - und nur dann - ist jedes der Systeme im Bezug zum anderen System ein Inertialsystem ↗

[6] Der Tower, englisch für Turm, ist tatsächlich oft ein Turm. Ganz oben befindet sich ein Raum von dem aus man das gesamte Flugplatzgelände gut einsehen kann. In diesem Raum aus werden der Flugplatz und seine Umgebung überwacht. Mit einem Radargerät oder den Daten von GPS kann auf einem Bildschirm für jedes Flugzeug der genaue Standort zu jedem Zeitpunkt angegeben werden. Siehe auch Tower ↗

[7] γ = 1 geteilt durch die Wurzel aus 1 - (v²)/(c²) gibt den Lorentzfaktor γ (Gamma). Der Lorentzfaktor kann also direkt aus der Relativitgeschwindigkeit v der zwei Systeme S und S' berechnet werden. Das kleine c steht für die Lichtgeschwindigkeit und ist eine konstante Zahl. Der Lorentzfaktor steht letztendlich für die Stärke der relativistischen Effekte. Je größer die Relativgeschwindigkeit, desto größer ist auch dieser Faktor. Für Beispielwerte siehe unter Lorentzfaktoren ↗

[8] Angenommen man steht an einem Bahnübergang. Von links nach rechts fährt dann ein Personenzug genau in Richtung Norden vorbei. Für den Beobachter am Bahnübergang fährt die Lok mit hoher Geschwindigkeit Richtung Norden. Nun stelle man sich vor, man laufe in demselben Zug in einem Waggon langsam Richtung Lok. Relativ zu dem Fahrgast bewegt sich die Lok langsam Richtung Süden. Welche Geschwindigkeitkeit die Lok hat, hängt ab vom Beobachter. Siehe auch Relativgeschwindigkeit ↗

[9] Ist die Relativgeschwindigkeit klein, was zum Beispiel für typische Bewegungsaufgaben aus der Physik rund um Schiffe, Züge, Flugzeuge oder auch Satelliten und Raketen gilt, dann nutzt man nicht die mathematisch aufwändige Lorentz-Transformation sondern die sehr viel einfachere Galilei-Transformation ↗

[10] Eine interessante Ausnahme ist die Entstehung des Magnetismus. Der Magnetismus ist ein relativistischer Effekt der an sich sehr langsamen Bewegungn von elektrischen Ladungen zu einem Beobachter. Man redet hier über wenige Zentimeter pro Sekunde. Dennoch machen sich hier Einsteinsche, das heißt relativistische Effekte bemerkbar. Das liegt daran, dass die beteiligten elektrostatischen Kräfte enorm hoch sind. Dass der Magnetismus ein relativistisches Phänomen ist zeigt die Abhängigkeit der Effekte von Geschwindigkeiten der Experimentatoren. Siehe dazu zum Beispiel den Artikel zur elektromagnetischen Lorentzkraft ↗

[11] Das hier angedeutete Experiment von Michelson und Morley stellte Wissenschaftler über Jahrzehnte vor ein nicht erklärbares Rätsel. Erst im Jahr 1905 brachte Einstein die Lösung. Siehe dazu auch Michelson-Morley-Experiment ↗