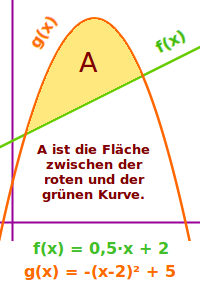
Fläche zwischen Kurven
Integralrechnung
Definition
Eine Fläche zwischen zwei Kurven oder Graphen wird innerhalb der Integralrechnung behandelt: Man hat zwei beliebige Graphen, die aber keine Lücken haben dürfen. Nun kann man zwei beliebige (verschiedene) senkrechte Striche durch das Koordinatensystem ziehen. Diese zwei Striche bilden den linken und rechten Rand der jetzt betrachteten Fläche. Der eine Graph bildet dann die obere Begrenzung, der andere die untere Begrenzung. Die ganze Fläche heißt dann: Flächen zwischen den Kurven beziehungsweise Flächen zwischen den Graphen. Das ist hier näher erklärt.
Von links bis rechts: das Intervall
- Man hat zwei Funktionen mit Graphen gegeben.
- Man betrachtet die Graphen in einem bestimmten Intervall.
- Intervall meint: von einem linken bis zu einem rechten x-Wert.
- Man zieht gedanklich eine senkrechte Linie durch die linke x-Stelle.
- Man zieht gedanklich eine senkrechte Linie durch die rechte x-Stelle.
- Man betrachtet die Graphen nur in diesem Intervall ↗
- Beachte auch die oft verschiedenen Intervallschreibweisen ↗
- Der linke und der rechte Rand sind dann die Integrationsgrenzen ↗
Die Fläche zwischen den Kurven
Im betrachteten Intervall schraffiert man alle Flächen, die zwischen den zwei Kurven (Graphen liegen). Das ist die Fläche zwischen den Kurven.
Die Größe der Fläche: der Flächenbetrag
Möchte man nur wissen, wie groß die Flächen zwischen den zwei Kurven ist, dann sucht man den sogenannten Flächenbetrag, auch absolute Fläche genannt. Das ist eine immer positive Zahl oder Null, aber niemals eine negative Zahl. Siehe auch Flächenbetrag ↗
Wie berechnet man die Fläche zwischen Kurven?
Dazu gibt es zwei sehr ähnliche Verfahren, die auch immer dasselbe Ergebnis liefern. Die Grundidee ist es, zuerst die Fläche unter der Kurve von dem oberen Graphen zu berechnen. Dann zieht man davon die Fläche unter der Kurve von dem unteren Graphen ab. Die so erhaltene Zahl ist der gesuchte Flächenbetrag. Die Rechenverfahren dazu sind erklärt unter Fläche zwischen Kurven berechnen ↗
