Fläche zwischen Kurven berechnen
Integralrechnung
© 2016
- 2025
Basiswissen
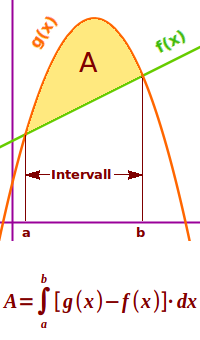
A = F(x)-G(x) über die Differenzenmethode: man hat zwei Graphen in einem Koordinatensystem gegeben. Gesucht ist die Fläche, die zwischen diesen zwei Graphen und zwei weiteren senkrechten Linien, den Integrationsgrenzen a und b liegt. Dazu ist hier eine Berechnungsmethode vorgestellt.
Aufgabenstellung
- Man hat die Graphen zweier Funktion f(x) und g(x) gegeben.
- Man soll die Flächen zwischen den Graphen im Intervall von a bis b berechnen.
- a und b sind Stellen auf der x-Achse, a ist weiter links als b.
- f(x) und g(x) können - müssen aber keine - Schnittpunkte im Intervall a bis b haben.
- Man sucht die Fläche, die zwischen den beiden Kurven (Graphen) liegt.
Keine Schnittpunkte
- Überprüfe, ob es zwischen a und b Schnittpunkte von f(x) und g(x) gibt.
- Falls ja, lies unten weiter. Falls nein, lies hier weiter:
- Überprüfe, welche Graph oben und welcher unten ist.
- Nehmen wir an, f(x) sei im Intervall überall oberhalb von g(x).
- Bestimme ∫f(x)·dx, also die Aufleitung F(x) zu f(x)
- Bestimme ∫g(x)·dx, also die Aufleitung G(x) zu g(x)
- Berechne das Integral m (als Zahlenwert) von F(x) in den Grenzen von a bis b.
- Berechne das Integral n (als Zahlenwert) von F(x) in den Grenzen von a bis b.
- Berechne die Differenz m-n. Der Zahlenwert ist die gesucht Fläche.
Schnittpunkte
- Haben f(x) und g(x) im Intervall a bis b einen oder mehrere Schnittpunkte, gehe so vor:
- Berechne die Schnittpunkte von f(x) und g(x).
- Berechne die einzelnen Fläche zwischen den Schnittpunkten und den Grenzen a und b.
- Addiere am Ende die Einzelflächen zur Gesamtfläche auf.
Aufgaben dazu
Einige Übungsbeispiele sind hier als Aufgabensammlung (Quickcheck) zusammengestellt. Zu allen Aufgaben gibt es immer auch eine Lösung. Direkt zu den Aufgaben geht es über => qck