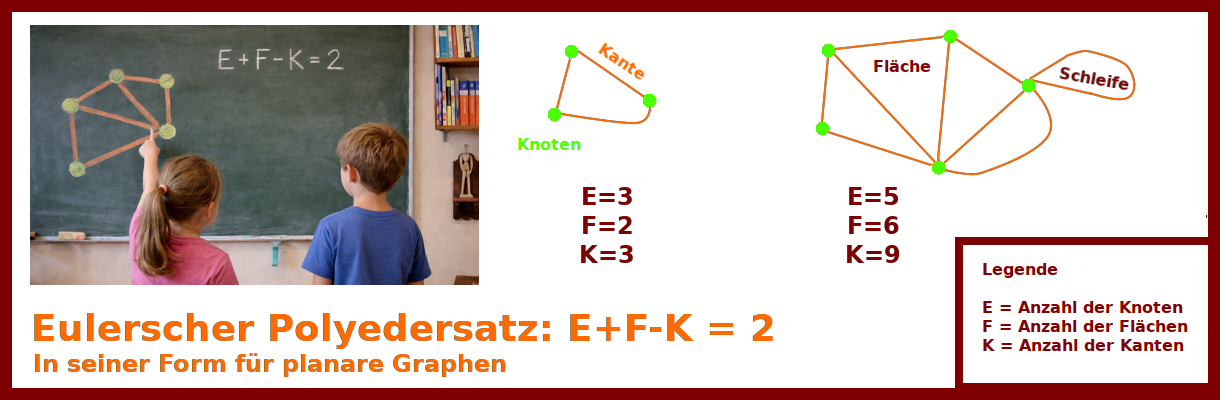
Eulerscher Polygon-Versuch
Logik
© 2026
Grundidee
Echte Mathematik ab der Klasse 1? Das geht mit einem einfachen aber tiefgründigen Beispiel aus der Graphentheorie. Je nach Interesse ist das etwas für 5 Minuten oder auch eine ganze Stunde: man zeichnet Punkte an die Tafel. Dann zeichnet man Linien, die in einem Punkt anfangen und irgendwo in einem Punkt auch wieder enden oder ins Leere gehen. Dann zählt man die Punkte, die Linien und die so erzeugten Teilflächen und macht damit eine einfache Rechnung. [4] Interessant ist das Ergebnis.
Anleitung
Graph zeichnen
- Zeichne beliebig viele Punkte auf ein Blatt Papier oder eine Tafel.
- Diese Punkten nennt man dann Knoten. Wir nennen sie hier Ecken.
- Wenn es mehr als einen Ecke gibt: verbinde die Ecken mit Linien.
- Die Linien zwischen den Ecken heißen Kanten.
- Eine Kante hat immer einen Anfangs- und einen Endknoten.
- Eine Kante darf auch in ihrem Startknoten enden. Das gibt dann eine Schleife.
- Eine Kante darf niemals eine andere Kante kreuzen, also durch sie hindurch gehen. [2]
- Zischen zwei Ecken dürfen auch mehreren Kanten gezeichnet werden.
- Es muss einen Weg von jeder Ecke zu jeder anderen Ecke geben. [3]
- Die ganze Figur nennt man dann einen Graphen.
Zählen
- Zähle für den Graphen die Anzahl von Ecken, Kanten und Flächen.
- Der Zeichenhintergrund gilt als eine Fläche.
- Jede umrandete Fläche wird dann hinzuaddiert.
- Beispiel: ein Dreick hat zwei Flächen: eine innen und eine außen.
- Schreibe dann als Ergebnis auf:
- E = ______ <- deine Zahl für die Anzahl der Ecken
- F = ______ <- deine Zahl für die Anzahl der Flächen
- K = ______ <- deine Zahl für die Anzahl der Kanten
Rechnen
Jetzt rechne: Anzahl Ecken plus die Anzahl der Flächen minus die Anzahl der Kanten. Schreibe die Rechnung mit dem Ergebnis an den Graphen dazu. Man kann die Rechnung auch kurz als Formel aufschreiben:
- E+F-K = _____ <- das Rechenergebnis
Zeichne jetzt möglichst viele verschiedene Graphen wie oben beschrieben. Du wirst merken, dass du irgendwann gar nicht mehr rechnen musst. Du wirst schon vorher ohne zu rechnen wissen, was herauskommt.
Erkunden
Wenn man sich genau an die Anleitung für das Zeichnen hält, kommt immer dieselbe Zahl heraus. Doch wenn man die Regeln für das Zeichnen etwas lockert, können auch andere Dinge passiert. Was passiert mit dem Rechenwergebnis, wenn …
- die Kanten sich auch kreuzen dürfen?
- es Ecken mit nur einer Kante geben darf?
- man die Ecken dreidimensional im Raum verteilt?
Kann man für diese Fälle wiederum neue Vorhersagen für das Rechenergebnis machen? Dieser Versuch wurde schon im 18. Jahrhundert, vor über 250 Jahren gemacht. Er führte zu sehr tiefsinnigen mathematischen Gedanken.
Fußnoten
- [1] Eine ausführliche Beschreibung eines Workshops mit acht Jahre alten Grundschülerinnen zum Eulerschen Polyedersatz findet man in: Joel David Hamkins: Math for eight-year-olds: graph theory for kids! 6. April 2015. Online: https://jdh.hamkins.org/math-for-eight-year-olds/
- [2] Beispiel: Man hat die vier Ecken eines Quadrats als vier Knoten und die vier Randlinien des Quadrats als Kanten. Dann zeichnet man die zwei Diagonalen im Inneren noch als zusätzliche Kanten hinzu. Diese zwei Diagonalen kreuzen sich jetzt. Man kommt auf: E=4, F=5, K=6 und damit wird E+F-K zu 4+5-6=3, also nicht mehr 2. Man kann den Mangel aber beheben, indem man den Kreuzungspunkt der zwei Diagonalen zu einem Ecken macht. Dann hat man: E=5, F=5, K=8. Und damit wird E+F-K zu 5+5-8=2.
- [3] Diese Bedingung stellt sicher, dass die Graphen zusammenhängend sind. Der Polyedersatz gilt nur für zusammenhängende Graphen. Zwei unverbundene Dreiecke nebeneinander kommen nicht auf das Ergebnis 2: Für zwei Dreiecke nebeneinander erhält man: E=6, F=3, K=6 und damit: E+F-K gibt 6+3-6=3. Dabei wurden insgesamt 3 Flächen gezählt: je eine Fläche innerhalb eines jeden Dreiecks und dann noch die beide Dreiecke umgebende Zeichenfläche.
- [4] "Für Polyeder ohne durchgehende Löcher (Polyeder vom Geschlecht Null), insbesondere also für konvexe Polyeder gilt: f+e-k=2." In: der Artikel "Eulersche Polyederformel". Guido Walz: Spektrum Lexikon der Mathematik. Band 2: Eig bis Inn; 2001; ISBN: 3-8274-0437-7.