Widerspruchsfrei zu anerkannten Aussagen
In der Mathematik und Logik gelten Aussagen als „wahr“ wenn sie keine Widersprüche zu anderen als wahr anerkannten Aussagen erzeugen und auch in sich selbst widerspruchsfrei sind. Das Gegenteil von wahr ist dann falsch. In der Naturwissenschaften wird das Wort eher nicht verwendet. Unterschiedliche Bedeutungen je nach Fach stehen unter => Wahrheitskriterium
Astronomie | Kaufmannswesen
Ein Jahr ist die Zeit, die die Erde benötigt, um einmal ganz um die Sonne zu laufen. Ein Jahr hat genau 12 Monate oder 52 Wochen und in etwa 365 Tage. => Ganzen Artikel lesen …
Abstimmung
Eine Wahl ist eine Entscheidung für eine oder wenige von mehreren Möglichkeiten. In der Politik wählt zum Beispiel eine Bevölkerung Staatsoberhäupter, Abgeordnete oder Stadträte. Siehe auch => Prozentrechnung
Wehr
Wasserbau
Eine Stauung eines Flusses oder Fließgewässers. Das Wasser oberhalb des Wehres heißt Oberwasser. In Fließrichtung unterhalb des Wehres nennt man das Wasser auch Unterwasser. Wehre erfüllen verschiedene Zwecke. Die Wasserströmung im unteren Bereich ist oft lebensgefährlich. => Ganzen Artikel lesen …
Ist ein anderes Wort für falsch.
Baumdiagramm
Dort wo ein Baumdiagramm endet liegen die Ausgänge. Die Ausgänge sind meistens ganz unten oder ganz rechts in einem Baumdiagramm zu sehen. Die Wahrscheinlichkeiten, die zu jedem einzelnen Ausgang gehören, nennt man entsprechend Ausgangswahrscheinlichkeiten. => Ganzen Artikel lesen …
Bedingte Wahrscheinlichkeit
Definition
Die Wahrscheinlichkeit, dass jemand mit blonden Haaren blaue Augen hat ist höher, als die Warscheinlichkeit, dass jemand mit schwarzen Haaren blaue Augen hat: die Haarfarbe bedingt (beeinflusst) die Wahrscheinlichkeit für Blauäugigkeit. Die Augenfarbe Blau ist damit eine bedingte Wahrscheinlichkeit. Dieser Begriff wird in der Stochastik rechnerisch gefasst und hier kurz erklärt. => Ganzen Artikel lesen …
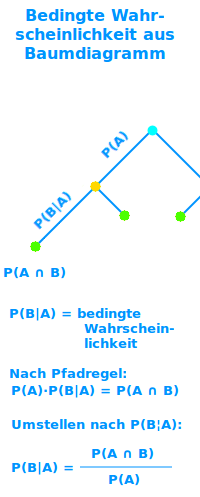Bedingte Wahrscheinlichkeit aus Baumdiagramm
Stochastik
Für zweistufige Zufallsversuche kann man aus einem Baumdiagramm immer bedingte Wahrscheinlichkeiten berechnen. Das ist hier erklärt. => Ganzen Artikel lesen …
Bedingte Wahrscheinlichkeit aus Vierfeldertafel
Stochastik
Aus einer Vierfeldertafel kann man immer bedingte Wahrscheinlichkeiten berechnen. Dabei gibt es 8 Möglichkeiten. Diese sind hier kurz dargestellt. => Ganzen Artikel lesen …
Stochastik
Die Grundformel ist: P(A|B) = P(A∩B)/P(B). Diese Formel ist hier mit Legende kurz vorgestellt. => Ganzen Artikel lesen …
Methoden
Eine bedingte Wahrscheinlichkeit, zum Beispiel geschrieben als P(A|B), kann über Baumdiagramme, Vierfeldtafelen, eine Formel sowie auch über einen Versuch empirisch bestimmt werden. Diese Methoden sind hier kurz vorgestellt. => Ganzen Artikel lesen …
… mit einem Versuch, zum Beispiel => Bedingte Wahrscheinlichkeit über Bayes-Schüssel-Versuch
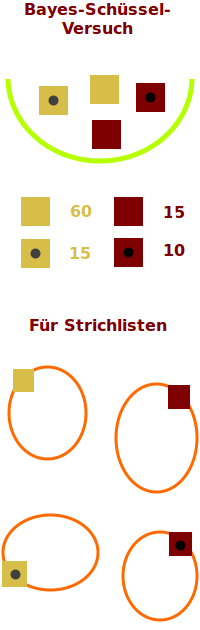Bedingte Wahrscheinlichkeit über Bayes-Schüsselversuch
Empirisch
Bedingte Wahrscheinlichkeiten kann man aus verschiedenen Angaben berechnen oder auch über einen Versuch direkt bestimmten. Hier ist ein beispielhafter Versuch mit einfachem Material vorgestellt. => Ganzen Artikel lesen …
Beispiele
Kopfbehaarung, Titanicopfer, Laktoseintoleranz: diese Phänomene hingen stark von anderen Phänomenen ab und sind damit Beispiele für bedingte Wahrscheinlichkeiten. Diese Beispiele - sowie noch weitere mehr - sind hier kurz vorgestellt. => Ganzen Artikel lesen …
… zum Beispiel als Kippfigur der berühmte => Necker-Würfel
Bornsche Wahrscheinlichkeitsinterpretation
Quantenphysik
In der Quantenphysik werden Naturgesetze nur noch als Wahrscheinlichkeitsaussagen interpretiert: die Wahrscheinlichkeiten geben an, wie oft man im Schnitt ein bestimmtes Messergebnis erhält, wenn ein Versuch sehr oft durchgeführt wird. Betrachtet man die Quantenphysik als letztendlich fundamental, werden alle Naturgesetze zu Wahrscheinlichkeitsgesetzen. Hier ist kurz vorgestellt, was daran so revolutionär sein soll. => Ganzen Artikel lesen …
Philosophie
Als Doppelte Wahrheit [1] wurde vorwurfsvoll die unterstellte geistige Haltung mittelalterlicher Philosophen im Umfeld der Pariser Universität bezeichnet. Dieser doppelten Wahrheit zufolge sollte es gleichzeitig eine philosophie und eine theologische Wahrheit geben können [12]. => Ganzen Artikel lesen …
… in der Stochastik die Wahrscheinlichkeit für ein => Elementarereignis
Empirische Wahrscheinlichkeit
Aus Versuch
Empirische Wahrscheinlichkeit heißt, dass die Wahrscheinlichkeit auf praktische Weise aus einem Versuch oder einer Beobachtung bestimmt wurde. Das Gegenteil einer empirischen Wahrscheinlichkeit ist eine theoretische Wahrscheinlichkeit. Empirisch heißt allgemein so viel wie „aus Erfahrung“ oder „durch Beobachtung“. Rechnerisch ist die empirische Wahrscheinlichkeit eng verbunden mit der relativen Häufigkeit. => Ganzen Artikel lesen …
Stochastik
Ein Ereignis kann sich aus mehreren Ergebnissen (Ausgängen) zusammensetzen. Eine Definition und Beispiele stehen unter => Ereignis
… heißt in der Stochastik oft nur kurz => Ereignis
… am Baumdiagramm, siehe unter => Summenregel für Ereignisse
… am Baumdiagramm, siehe unter => Summenregel für Ereignisse
Stochastik
Die Worte Erfolgswahrscheinlichkeit [1] und Trefferwahrscheinlichkeit werden in der Stochastik (Wahrscheinlichkeitsrechnung) mit gleicher Bedeutung, also als Synonyme gebraucht. Hier verwenden wir ds Wort => Trefferwahrscheinlichkeit
Farbwahrnehmung
Physik
Als Farbwahrnehmung bezeichnet man die Fähigkeit, mit Sinnesorganen verschiedene spektrale Zusammensetzungen von Licht unterscheiden zu können. Aber wie hängt das mit der physikalischen Idee von Wellen zusammen? [14] Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Stochastik
Die Gegenwahrscheinlichkeit eines Ereignisses ist die Wahrscheinlichkeit dafür, dass das Ereignis nicht eintritt. Die Wahrscheinlichkeit eines Ereignisses plus seine Gegenwahrscheinlichkeit geben in Summe immer genau 1 oder 100. Wenn beim Würfeln die Wahrscheinlichkeit für eine Sechs genau 1/6 ist, dann ist die dazugehörige Gegenwahrscheinlichkeit 5/6. Die Gegenwahrscheinlichkeit ist damit immer auch die Wahrscheinlichkeit für das sogenannte => Gegenereignis
… P(A∩B) von A und B => Schnittwahrscheinlichkeit
… im Zusammenhang mit einem Hypotesentest dasselbe wie der => Fehler erster Art
… ein anderes Wort für => bedingte Wahrscheinlichkeit
Psychologie
Zeigt man vier Monate alten Säuglingen gleichzeitig zwei unterschiedliche Filme aber nur die Tonspur zu einem der zwei Filme, dann schauen sie länger auf den passenden Film: die Kinder müssen hier eine Verbindung zwischen dem optischen Eindruck und dem akustischen Eindruck hergestellt haben. Eine solche Verbindung der Eindrücke verschiedener Sinneskanäle nennt man in der Entwicklungspsychologie eine kreuzmodale Wahrnehmung. Eng verwandt damit ist das Konzept => kreuzmodale Aufmerksamkeit
… gleich große Wahrscheinlichkeiten bei einem Versuch, mehr unter => Laplace-Wahrscheinlichkeiten
… gleich große Wahrscheinlichkeiten bei einem Versuch, mehr unter => Laplace-Wahrscheinlichkeiten
… alle Ergebnisse sind gleich wahrscheinlich, mehr unter => Laplace-Experiment
… gleich große Wahrscheinlichkeiten bei einem Versuch, mehr unter => Laplace-Wahrscheinlichkeiten
… heißt in der Stochastik oft nur kurz => Ereignis
