Strecken
Ãœbersicht
Strecken sind zum Einen die Längen von Linien. Die Linien können dabei gerade oder auch krumm und gezackt sein. Als Verb heißt strecken, etwas länger zu machen. Die verschiedenen Bedeutungen sind hier kurz vorgestellt. => Ganzen Artikel lesen …
Geometrie
In der Geometrie ist eine Strecke eine gerade Linie mit Anfang und mit Ende. Eine geometrische Strecke ist damit auch ein Stück einer Geraden, das von zwei Punkten begrenzt ist [1]. Wie lang eine Strecke ist bezeichnet man als Steckenlänge [2]. In dem Wort enthalten ist die Idee des Dehnens oder Langmachens [5]. Für weitere Bedeutungen und Beispiele siehe auch => Strecken
Stecker
Definition
Ein Stecker ist ein zu einer Steckdose gehörendes Verbindungselement elektrischer Stromkreise. Siehe auch => Elektrotechnik
… für eine Übersicht siehe den Artikel zum => strecken
Streichen
Bergbau
Immer auf gleicher Höhe bleibend: Streichen ist ein Fachwort aus der Geologie und dem Bergbau. Man meint damit, dass man sich gedanklich oder echt in einer unebenen Umgebung immer auf gleicher Höhe bewegt. Das Gegenteil wäre das => Einfallen
Definition
Ähnlich heißt in der Geometrie, dass zwei Objekte dieselbe Form haben, auch wenn sie unterschiedlich groß sind. Strecken, also gerade Linien mit Anfang und Ende, sind immer ähnlich zueinander. Hier ist erklärt warum das so ist. => Ganzen Artikel lesen …
… siehe unter => Bremswegformeln
… siehe unter => Bremswegformeln
Auseinanderziehen
Funktionen zu strecken heißt ihre Graphen zu strecken, also sie auseinanderzuziehen. Das Strecken ist ein Sonderfall von Graphentransformationen. Lies mehr unter => Graphen strecken
Definition und Anleitung
Von links nach rechts auseinanderziehen: hier steht was diese Streckung für den Graphen bedeutet, wie das mit der Funktionsgleichung zusammenhängt und wie man jede beliebige Funktionsgleich so ändert, dass sie danach von links nach recht entlang der x-Achse gestreckt ist. => Ganzen Artikel lesen …
Graph entlang y-Achse strecken
Anleitung
Von oben nach unten auseinanderziehen, dadurch erscheint der Graphe schmäler und höher. Hier steht auch, wie das mit der Funktionsgleichung zusammenhängt. => Ganzen Artikel lesen …
… steiler machen: => Graphen transformieren
Funktionen
Strecken heißt für Funktionsgraphen: auseinanderziehen und damit länger machen, ohne dass sich dabei aber etwas an der Breite ändert. Man unterscheidet zwei Fälle. => Ganzen Artikel lesen …
Anleitung
Man klammert jedes x im Funktionsterm ein und teilt es dann durch eine Zahl größer 1 oder kleiner -1: das Ergebnis ist eine Streckung entlang der x-Achse. => Ganzen Artikel lesen …
Anleitung
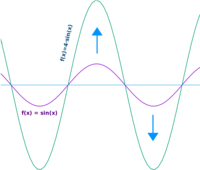
Streckt man eine Parabel in einem xy-Koordinatensystem entlang der y-Achse, erscheint sie hinterher höher und schmaler als vorher. Anschaulich gesprochen zieht man sie zwischen unten und oben auseinander in die Höhe. Rechnerisch streckt man eine Parabel entlang der y-Achse dadurch, dass man den ganzen Funktionsterm mit einer Zahl multipliziert, die entweder größer ist als 1 (z. B. 4) oder die kleiner ist als -1 (z. B. -4). => Ganzen Artikel lesen …
An x- und an der y-Achse
Die Streckung einer Parabel ist ein Sonderfall einer sogenannten Transformation und meint hier eine Dehnung, ein Auseinanderziehen. Die Streckung ist damit eine Art Gegenteil des Stauchens, also des Zusammendrückens. Eine Parabel als Graph einer Funktion kann sowohl entlang der y-Achse als auch entlang der x-Achse gestreckt werden. Beide Verfahren sind hier kurz vorgestellt. => Ganzen Artikel lesen …
… Funktionsterm mal Streckfaktor => Parabel strecken
… Funktionsterm mal Streckfaktor => Parabel strecken
… Funktionsterm mal Streckfaktor => Parabel strecken
… Funktionsterm mal Streckfaktor => Parabel strecken
… Funktionsterm mal Streckfaktor => Parabel strecken
Startstrecken
Fliegerei
Von 10 Metern für einen Tragschrauber bis zu 3,4 Kilometern für die Concorde: die Startstrecke ist die übliche Strecke, die ein Luftfahrzeug braucht, um die nötige Geschwindigkeit für ein Abheben zu erreichen. Hier stehen einige Beispiele. => Ganzen Artikel lesen …
Streckenausbau
Bergbau
Unter Tage, das heißt unter der Erdoberfläche, gebaute tunnelartige Strecken würden von alleine irgendwann einstürzen oder vom umliegenden Gebirge langsam zugedrückt werden. Um das zu verhindern, kann man die Strecke von innen Mauern oder auch mit Stahlbögen abstützen. Man spricht von einem Streckenausbau. Eine besondere Art des Ausbaus ist der => Ankerausbau
Technischer Fachbegriff [Bergbau]
… Strich nach Augenmaß dritteln => Strich dritteln
Technischer Fachbegriff [Bergbau]
Streckenförderung
Horizontale Materialbewegung
Als Streckenförderung bezeichnet man im Bergbau das annähernd horizontale Bewegen von Materialien, mineralischen Rohstoffen, Produkten und Versatz in untertägigen Strecken und Stollen. Nicht zur Streckenförderung gehört der Transport von Werkzeugen, Bauteilen und Menschen. Die Streckenförderung beginnt mit dem Befüllen der Fördergefäße und endet am Füllort des Schachtes. Beim Förderstollen endet die Streckenförderung am Stollenmundloch. => Ganzen Artikel lesen …
Definition
In der Geometrie ist eine Strecke eine gerade Linie mit einem Anfangs- und einem Endpunkt. Ihre Länge ist damit auch genauso groß wie der Abstand vom Anfang zum Ende der Strecke. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
Berechnung
Vektor aus dem Anfangs- und Endpunkt bilden und davon die Länge berechnen: eine Strecke in der Geometrie ist eine gerade Linie mit Anfang und Ende. Wie man die Länge mit Hilfe von Vektoren berechnet ist hier kurz erklärt. => Ganzen Artikel lesen …
Streckenlängen berechnen
Beispiele
Eine Strecke ist immer eine gerade Linie mit Anfang und Ende. Typische Streckenlängen können Flugstrecken, Dreieckshöhen, Fallstrecken oder Hochhaushöhen sein. Hier stehen einige Grundideen zur Berechnung von solchen Streckenlängen. => Ganzen Artikel lesen …
… siehe unter => Streckenmittelpunkt
Geometrie
Eine Strecke ist in der Geometrie eine gerade Linie. Sie hat einen Anfang und ein Ende. Der Mittelpunkt einer solchen Strecke ist ein Punkt, der genauso weit vom einen Ende entfernt ist wie vom anderen Ende. Er teilt die Strecke in zwei gleich lange Hälften. Siehe auch => Streckenmittelpunkt bestimmen
Verfahren
Geometrisch über die Mittelsenkrechte, rechnerisch über den Koordinatenmittelpunkt und als dritte Möglichkeit über die Vektorrechnung: hier stehen verschiedene Möglichkeiten, die Mitte einer geraden Strecke zu bestimmen. => Ganzen Artikel lesen …
… ein anderes Wort für die => Mittelsenkrechteür die => Mittelsenkrechte
Streckenteiler
Werkzeug
Als Streckenteiler bezeichnet man ein zirkelähnliches spreizbares Gerät, das eine Strecke in bis zu 10 gleich lange Abschnitte teilen kann. Die Mechanik nennt man auch eine Nürnberger Schere. Siehe auch => zehnteln
