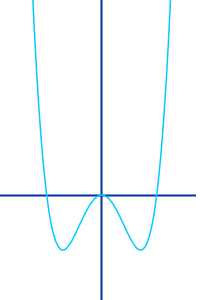
Quartische Funktion
f(x)=T(x⁴)
Ganzrationale Funktion mit höchstens x hoch 4: als quartisch bezeichnet man eine Funktion, die man in die Form f(x) = a·x⁴ + b·x³ + c·x^2 + d·x + e bringen kann. Ein anderer, gleichbedeutender Name ist ganzrationale Funktion vierten Grades. Das Wort quartisch steht für 4 und bezeichnet die höchste vorkommende Potenz der unabhängigen Variablen x. => Ganzen Artikel lesen …
Funktion
f(x)
f(x)=4x+8 ist eine typische mathematische Funktion: man kann für x eine beliebige Zahl einsetzen. Die Rechnung gibt dann einen y-Wert als Ergebnis der eindeutig dem eingesetzten x-Wert zugeordnet ist. Das ist die Grundidee einer Funktion. Der Gedanke wird hier ausführlich erklärt. => Ganzen Artikel lesen …
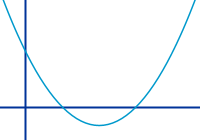Quadratische Funktion
f(x)=ax²+bx+c
Jede Funktion deren Gleichung man auf die Form f(x)=ax²+bx+c bringen kann heißt quadratisch. Das a darf irgendeine Zahl außer der Null sein. b und c dürfen auch - müssen aber nicht - Null sein. Der dazugehörige Graph ist immer eine (quadratische) Parabel. => Ganzen Artikel lesen …
Beispiele
Eine quartische (hoch 4) Funktion ist eine ganzrationale Funktion vom Grad 4. Hier stehen Beispiele dafür. Für die Definition siehe unter => quartische Funktion
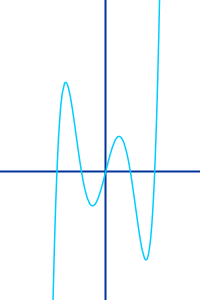Quintische Funktion
Hoch 5
Die höchste Potenz von x ist die 5: eine quintische Funktion heißt auch ganzrationale Funktion fünften Grades. Ihr Graph ist eine quintische Parabel. Die Funktion ist hier kurz vorgestellt. => Ganzen Artikel lesen …
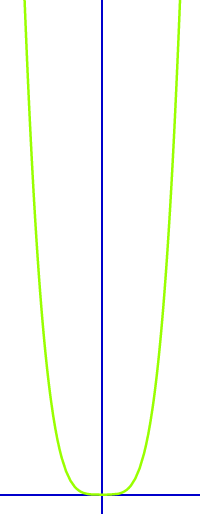Reinquartische Funktion
Definition
Jede Funktion - und nur eine solche Funktion - die man umformen kann in f(x) = x^4 + b heißt reinquartisch. Die Nullstellen lassen sich vergleichsweise einfache berechnen. Hier steht eine kurze Einführung dazu. => Ganzen Artikel lesen …
… hoch-vier-Funktion => quartische Funktion ableiten
… Graph einer Funktion mit x-hoch-4 => Parabel vierten Grades
… z. B. von x^4, siehe unter => Parabel vierter Ordnung
… sieht aus wie eine normale Parabel, ist aber keine und heißt deshalb => Pseudonormalparabel
… z. B. von x^4, siehe unter => Parabel vierter Ordnung
… siehe => Nullstellen von quartischen Funktionen bestimmen
… siehe => Nullstellen von quartischen Funktionen bestimmen
… siehe => Nullstellen von quartischen Funktionen bestimmen
… siehe => Nullstellen von quartischen Funktionen bestimmen
… siehe => Nullstellen von quartischen Funktionen bestimmen
… siehe => Nullstellen von quartischen Funktionen bestimmen
… mehrere Methoden unter => Nullstellen von quartischen Funktionen bestimmen
Anleitung
f(x) = 2x⁴+4x³-5x²+8x-20 wird abgeleitet zu f'(x) = 8x³-10x+8: Eine quartische Funktion wird oft auch ganzrationale Funktion vierten Grades genannt. Die höchste Potenz von x ist die Zahl 4. Bei der Ableitung entsteht immer eine kubische Funktion (hoch 3). Das ist hier an einem Zahlenbeispiel erklärt. => Ganzen Artikel lesen …
… z. B. von x^4, siehe unter => Parabel vierter Ordnung
… siehe unter => y-Achsenabschnitt von quartischen Funktionen
… siehe unter => y-Achsenabschnitt von quartischen Funktionen bestimmen
… z. B. von x^4, siehe unter => Parabel vierter Ordnung
… mehrere Methoden unter => Nullstellen von quartischen Funktionen bestimmen
… mehrere Methoden unter => Nullstellen von quartischen Funktionen bestimmen
… sieht aus wie eine normale Parabel, ist aber keine und heißt deshalb => Pseudonormalparabel
… siehe unter => y-Achsenabschnitt von quartischen Funktionen
… siehe unter => y-Achsenabschnitt von quartischen Funktionen bestimmen
