Basiswissen

Jede Funktion - und nur eine solche Funktion - die man umformen kann in f(x) = x^4 + b heißt reinquartisch. Die Nullstellen lassen sich vergleichsweise einfache berechnen. Hier steht eine kurze Einführung dazu.

Bildbeschreibung und Urheberrecht — f(x) = x^4☛

Beispiele

f(x) = 2x⁴ + 16

f(x) = 2x⁴ - 16

f(x) = x⁴

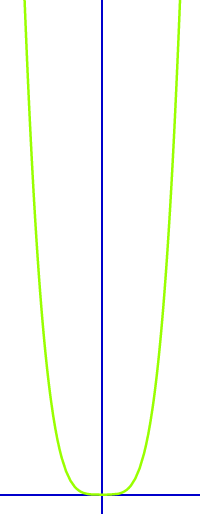
Graph

Heißt Parabel vierter Ordnung ↗

Ist eine Art Pseudonormalparabel ↗

Ist achsensymmetrisch zur y-Achse.

Das b ist der y-Achsenabschnitt.

Kann keine, eine oder zwei Nullstellen haben.

Hat immer genau einen Extrempunkt.

Kann keine Wendepunkte haben.

Kann keine Sattelpunkte haben.

Gegenbeispiele

f(x) = x^4 + x²

f(x) = 2x³ + x^4 - 1

Tipp

f(x) = x^4 - 12 geht auch, weil ...

f(x) = x^4 - 12 ist wie x^4 + (-12)

Nullstellen

Eine solche Funktion kann keine, eine oder genau zwei Nullstellen haben. Mehr ist nicht möglich. Die Berechnung ist vergleichsweise einfach. Lies mehr unter Nullstellen von quartischen Funktionen bestimmen ↗