Anleitung
Man hat einen Vektor oder auch zwei Vektoren gegeben und soll dazu einen weiteren Vektor angeben, der orthogonal, das heißt senkrecht, also im 90°-Winkel, zu den gegebenen Vektoren steht. Hier sind verschiedene Verfahren dazu kurz vorgestellt. => Ganzen Artikel lesen …
Etwas mit 90°-Winkel
Eine Gerade, Strecke oder Ebene kann eine Orthogonale zu etwas anderem sein. Das meint dann, dass sie mit einem 90°-Winkel (also senkrecht) auf etwas anderes trifft. Eine Gerade kann zum Beispiele eine Orthogonale von einer anderen Geraden sein. Man unterscheidet dabei 2D- und 3D-Koordinatensysteme. => Ganzen Artikel lesen …
⊗☉↗⮅ Arten und Einteilung
Vektoren sind gedachte Pfeile in einem 2D-, 3D- oder höherem Koordinatensystem. Sie werden oft aus zwei oder drei Zahlen zusammengesetzt, etwa (4|3|5). => Ganzen Artikel lesen …
 Bestimmen
Bestimmen
(Irgendwie) herausfinden
Bestimmen heißt: etwas herausfinden, wobei der genaue Weg dazu aber offen gelassen wird. Man kann etwas über eine Berechnung, über Schätzen, über Recherchieren oder sonstwie bestimmen. => Ganzen Artikel lesen …
Anleitung
Die Vektoren (2|3|4) und (3|2|-3) sind zueinander orthogonal: immer dann - und auch nur dann - wenn das Skalarprodukt von zwei Vektoren genau 0 ergibt, dann sind die zwei Vektoren zueinander orthogonal, sie bilden dann also einen rechten Winkel. Das ist hier kurz mit Beispielen vorgestellt. => Ganzen Artikel lesen …
Übersicht
Ein Normalenvektor ist immer ein Vektor, der senkrecht, also im 90°-Winkel, auf etwas anderem stehen soll. Normalenvektoren werden vor allem im Zusammenhang mit Ebenen und Geraden behandelt, aber auch in der Physik. Beides ist hier kurz vorgestellt. => Ganzen Artikel lesen …
… Gerade senkrecht auf Punkt von Graph => Normalengleichung aufstellen
 Orthogonale Vektoren
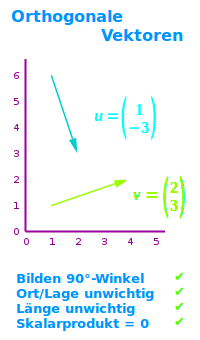
Orthogonale Vektoren
90°-Winkel
Orthogonale Vektoren sind hier zwei oder mehr Vektoren, die zueinander orthogonal, das heißt rechtwinklich sind, also einen 90°-Winkel einschließen. Das Skalarprodukt solcher zueinander orthogonaler Vektoren ist immer 0. => Ganzen Artikel lesen …

