 Orthogonale Vektoren
Orthogonale Vektoren
90°-Winkel
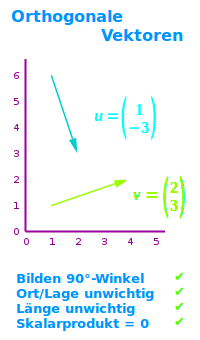
Orthogonale Vektoren sind hier zwei oder mehr Vektoren, die zueinander orthogonal, das heißt rechtwinklich sind, also einen 90°-Winkel einschließen. Das Skalarprodukt solcher zueinander orthogonaler Vektoren ist immer 0. => Ganzen Artikel lesen …
Etwas mit 90°-Winkel
Eine Gerade, Strecke oder Ebene kann eine Orthogonale zu etwas anderem sein. Das meint dann, dass sie mit einem 90°-Winkel (also senkrecht) auf etwas anderes trifft. Eine Gerade kann zum Beispiele eine Orthogonale von einer anderen Geraden sein. Man unterscheidet dabei 2D- und 3D-Koordinatensysteme. => Ganzen Artikel lesen …
⊗☉↗⮅ Arten und Einteilung
Vektoren sind gedachte Pfeile in einem 2D-, 3D- oder höherem Koordinatensystem. Sie werden oft aus zwei oder drei Zahlen zusammengesetzt, etwa (4|3|5). => Ganzen Artikel lesen …
Vektoren
Zwei Vektoren sind zueinander orthonormal, wenn sie sowohl senkrecht aufeinander stehen, also das Skalarprodukt haben sowie zusätzlich auch beide noch die Länge (Betrag) Eins haben. Siehe auch => orthogonal
Vektorrechnung
Zwei Ebenen sind genau dann orthogonal zueinander, wenn ihre Normalnvektoren zueinander orthogonal sind. Ob die zwei Normalenvektoren zueinander senkrecht sind kann man mit Hilfe des Skalarproduktes überprüfen (muss Null ergeben). Mehr zum Hintergrund, siehe unter => Normalenform der Ebene
3D-Geraden
Zwei Geraden in einem xy-Koordinatensystem stehen orthogonal zueinander, wenn sie in ihrem Schnittpunkt einen 90°-Winkel bilden. Zwei Geraden in einem xyz-Koordinatensystem stehen orthogonal zueinander, wenn das Skalarprodukt ihrer Richtungsvektoren 0 ergibt. Beide Fälle sind hier kurz erklärt. => Ganzen Artikel lesen …
Anleitung
Die Vektoren (2|3|4) und (3|2|-3) sind zueinander orthogonal: immer dann - und auch nur dann - wenn das Skalarprodukt von zwei Vektoren genau 0 ergibt, dann sind die zwei Vektoren zueinander orthogonal, sie bilden dann also einen rechten Winkel. Das ist hier kurz mit Beispielen vorgestellt. => Ganzen Artikel lesen …
Anleitung
Man hat einen Vektor oder auch zwei Vektoren gegeben und soll dazu einen weiteren Vektor angeben, der orthogonal, das heißt senkrecht, also im 90°-Winkel, zu den gegebenen Vektoren steht. Hier sind verschiedene Verfahren dazu kurz vorgestellt. => Ganzen Artikel lesen …
… stehen senkrecht aufeinander, Skalarprodukt ist Null, mehr unter => Orthogonale Vektoren

