Lernskript
Die Abkürzung lsk steht im Rhetos-Lexikon für Lernskripte. Lernskripte bestehen meist aus mehreren Seiten, die man auch ausdrucken kann. => Ganzen Artikel lesen …
… Kurz für => Kaufmännische Steuerung und Kontrolle
… in der Didaktik ein Leistungskurs, siehe auch => Abi
Lok
🚅 Ein Schienenfahrzeug mit Motor, oft auch Lokomotive genannt
Lok ist eine Abkürzung von Lokomotive: auf Deutsch: die Bewegende, die Ortsverändernde. Mit Lok bezeichnet man die Zugmaschine einer Eisenbahn. Beispiele stehen unter => Loks
… also Lernskripte, siehe unter => lsk
… [unübliche] Abkürzung für => System kubischer Gleichungen
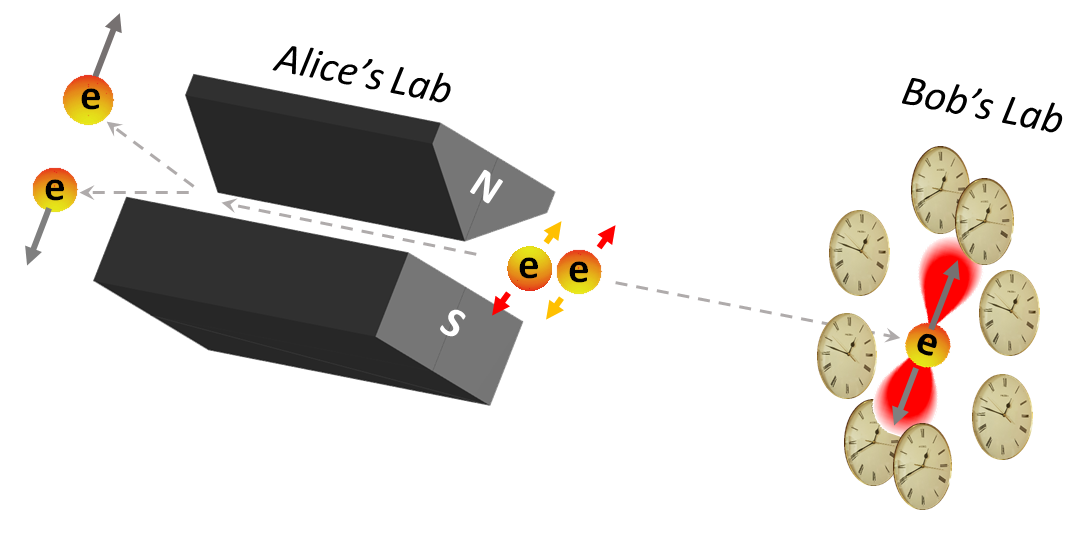Einstein-Podolsky-Rosen-Paradoxon
Physik
Das Einstein-Podolsky-Rosen-Paradoxon, kurz auch EPR war zunächst ein Gedankenexperiment. [1] Es kann heute experimentell nachgestellt werden. [9] Das EPR wirft bisher ungelöste Fragen auf, was man eigentlich mit dem Sein oder der Existenz eines physikalischen Objektes meint. Insbesondere bedrängen die experimentellen Befunde die strikte Trennbarkeit von beobachtenden Subjekten und beobachteten Dingen. => Ganzen Artikel lesen …
… Formel für radioaktiven Zerfall, siehe unter => Zerfallsgesetz
Beispiele
Monde, Planeten, Sonnen aber auch Asteroiden oder Kometen bezeichnet man als Himmelskörper: jeder natürliche oder künstliche Gegenstand, der sich von der Erde aus gesehen außerhalb der Atmosphäre befindet kann als Himmelskörper bezeichnet werden. Dazu stehen hier kurz aufgelistet einige Beispiele. => Ganzen Artikel lesen …
Astronomie
Als Himmelskugel [1], Himmelsglobus [2] oder Himmelssphäre [3] bezeichnet man ein rein gedankliches Modell. Auf einer gedachten Glaskugel ordnet man alle Objekte des Himmels an. Der große Vorteil dieses Denkmodells ist, dass man das Denken in Längen- und Breitengraden wie von einem Globus der Erde auf die Astronomie übertragen kann. Das ist hier Schritt-für-Schritt erklärt. => Ganzen Artikel lesen …
Statistik
Temperaturen in einem Raum: man kann den Ausprägungen eines Merkmals sinnvoll Abstände zuordnen. Das ist hier erklärt. => Ganzen Artikel lesen …
… in der Statistik: anordenbar auf einer => Intervallskala
Statistik
Als Kardinal bezeichnet man eine Skala, bei der Zahlenangaben im mathematischen Sinn als Abstände oder auch Verhältnisse interpretiert werden können. Man unterscheidet zwei Arten, die Intervall- und die Verhältnisskal sid beide => Kardinalskalen
Statistik
Raumtemperaturen in Grad Celius passen zu einer Intervallskala, Raumtemperaturen in Kelvin zusätzlich auch zu einer Verhältnisskala:in der Statistik ist eine Kardinalskala eine Skala, bei der man Merkmale von Objekten auch mathematisch-rechnerisch als Zahlen deuten kann. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
Statistik
Definition: Merkmalsausprägungen werden in Gruppen zusammengefasst. Typische Beispiele sind Fellfarben für Tiere, Blutgruppen oder Nationalitäten. Die Definition sinnvoller Abständen ist nicht nötig. => Ganzen Artikel lesen …
Statistik
Kategorialskalen gruppieren statistische Objekte nach festen Eigenschaften. Abstände zueinander spielen dabei keine Rolle. Man unterscheidet die Nominal- von der Ordinalskala. => Ganzen Artikel lesen …
… in der Atomphysik die => Lebensdauer (Physik)
Nominalskala
Statistik
Statistische Objekte Einteilen nach Namen, Erdzeitaltern, Haarfarben oder Geschlecht: Nominalskala heißt, dass man zur statistischen Klassifzierung von Dingen nur Namen benutzt, nicht etwa messbare Größe wie Länge oder Gewicht. Das ist hier näher erklärt. => Ganzen Artikel lesen …
Beispiel für nominal skalierte Merkmale eines Menschen:
Familienname: Janssen, Markowski, Beaujean => Ganzen Artikel lesen …
… passt am ehesten auf die statistische => Nominalskala
Ordinalskala
Statistik
Ordinalskala bezeichnet eine Anordnung von Dingen rein nach einer Rangfolge (Englisch: order). Ein Beispiel sind Steine, die man von weich nach hart anordnen kann. Es muss ein sinnvolles Kriterium für „mehr“ oder „weniger“ geben. => Ganzen Artikel lesen …
Beispiele
Ordinal meint so viel wie: in eine Reihenfolge gebracht. Dabei ist der Abstand zwischen den Elementen unwichtig. Es interessiert nur ein mehr oder weniger im gegenseitigen Verlgeich. => Ganzen Artikel lesen …
… bildet sinnvolle Reihenfolge, mehr unter => Ordinalskala
… ungelöstes Rätsel aus der Quantenphysik, siehe unter => EPR
Pottwalskelett
Wirbel
Der Pottwal ist ein typisches Wirbeltier. An seinem Skelett kan man gut erkennen, was das bedeutet: Vom Kopf Richtung Körperende zieht sich ein tragendes und stützendes aber in sich bewegliches Band aus einzelnen Knochen, den Wirbeln. Auch gut erkennt man die Fünfgliedrigkeit der Finger, die Schulterblätter, die beweglichen Kiefer und den die Innereien schützenden Brustkorbe. Siehe auch => Wirbeltier
… meint in der Statistik dasselbe wie => Verhältnisskala
… meint in der Statistik dasselbe wie => Verhältnisskala
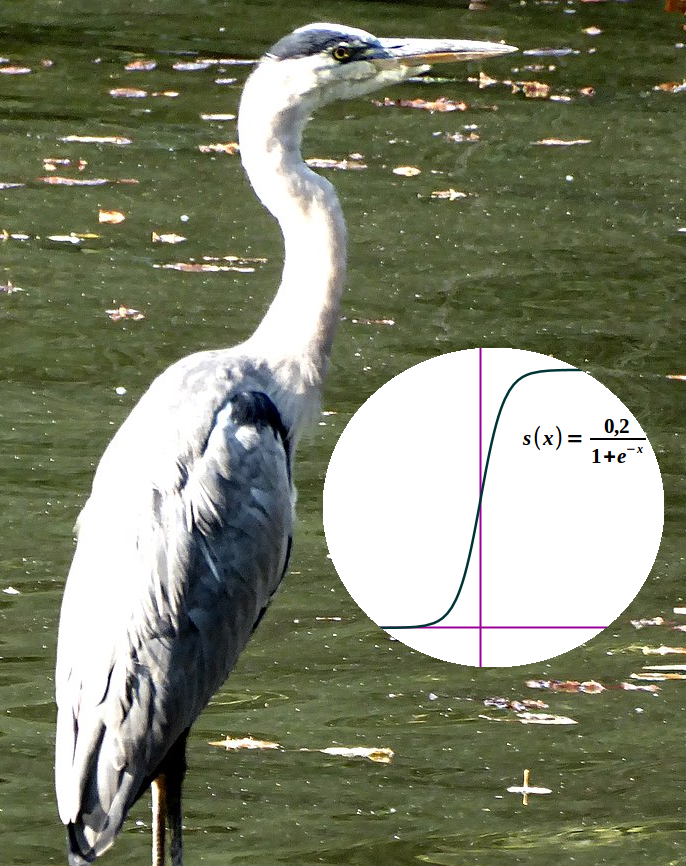Schwanenhalskurve
… stetiger Graph mit unterer und oberer Grenze, mehr unter => logistische Funktion
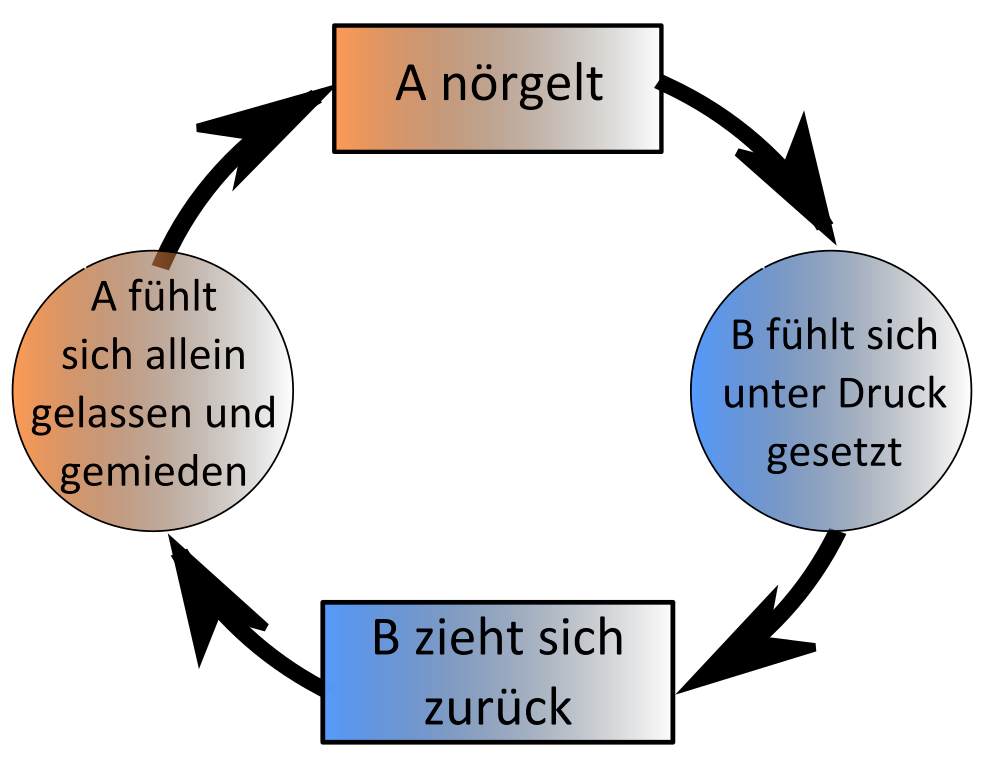Teufelskreis
Definition
A nörgelt an B herum ⭢ B zieht sich deshalb zurück ⭢ A nörgelt, dass B sich zurückzieht ⭢ und immer so weiter: als Teufelskreis bezeichnet man einen sich selbst verstärkenden Prozess, oft auch Abwärtsspirale oder positive Rückkopplung genannt. => Ganzen Artikel lesen …
… heißt laut Duden => Teufelskreis
Umrechnung
b = e^(-λ) ist die Formel zur Berechnung des Wachstumsfaktors aus einer bekannten Zerfallskonstanten λ. Die Zerfallskonstante kommt vor im sogenannten Zerfallsgesetz N(t) = N₀·e^(-λ·t) während der Wachstumsfaktor in der Darstellung über die erweiterte Exponentialfunktion N(t) = N₀·b^t verwendet wird. Für die umgekehrte Rechnung siehe unter => Zerfallskonstante aus Wachstumsfaktor
Zerfallskonstante
Definition
Die Zerfallskonstante λ gehört ins Gebiet der Atom- und Kernphysik. Zerfallskonstante, die Konstante λ im Exponentialgesetz des radioaktiven Zerfalls (Zerfallsgesetz). Sie gibt den pro Sekunde zerfallenden Bruchteil der vorhandenen Atomanzahl N an. [1] Die Einheit ist pro Sekunde, kurz auch geschrieben als s⁻¹. => Ganzen Artikel lesen …
Umrechnung
λ = -ln(b) ist die Formel zur Berechnung der Zerfallskonstanten λ aus einem bekannten Wachstumsfaktor b. Die Zerfallskonstante kommt vor im Zerfallsgesetz N(t) = N₀·e^(-λ·t) während der Wachstumsfaktor in der Darstellung über die erweiterte Exponentialfunktion N(t) = N₀·b^t verwendet wird. Für die umgekehrte Rechnung siehe unter => Wachstumsfaktor aus Zerfallskonstante
Physik
Die Zerfallskonstante λ wird oft im Zusammenhang mit dem radioaktiven Zerfall behandelt. Hier stehen kurz erklärt zwei Varianten zu ihrer Berechnung. => Ganzen Artikel lesen …
… siehe unter => Zerfallskonstante berechnen
