Anleitung
Zum Beispiel f(x) = (4x^3)/(2x^5-8): Als gebrochenrational (wird als ein Wort geschrieben) bezeichnet man Funktionen, deren Funktionsterm aus einem Zähler und einem Nenner bestehen. Sowohl der Zähler als auch der Nenner sind dabei jeweils eine eigene ganzrationale Funktion vom Grad 1 (linear) oder höher. Die Grundidee zur Ableitung ist die sogenannte Quotientenregel. => Ganzen Artikel lesen …
Funktion
f(x)
f(x)=4x+8 ist eine typische mathematische Funktion: man kann für x eine beliebige Zahl einsetzen. Die Rechnung gibt dann einen y-Wert als Ergebnis der eindeutig dem eingesetzten x-Wert zugeordnet ist. Das ist die Grundidee einer Funktion. Der Gedanke wird hier ausführlich erklärt. => Ganzen Artikel lesen …
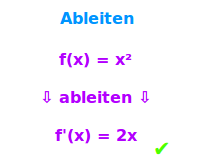
Ableiten
Verfahren
Ableiten heißt f'(x) bilden: Ableiten im engeren Sinn heißt: Für einen Funktionsgraphen an einem Punkt die Steigung bestimmen. Im allgemeineren Sinn steht es dafür, die Ableitungsfunktion f'(x) zu bestimmen. Hier sind Regeln zur Bestimmung von f'(x) zusammengestellt. => Ganzen Artikel lesen …
Gebrochenrationale Funktionen
Definition
f(x) = (4x-2)/(x²-1): eine gebrochenrationale Funktion hat als Funktionsterm einen Bruch - oder kann in eine solche Form umgewandelt werden. Dabei sind sowohl der Zähler- als auch der Nennerterm ganzrationale Terme. Das ist hier erklärt. => Ganzen Artikel lesen …
Methoden
f(x)=4x³-3x²+4x-22 wird zu f'(x)=12x²-6x+4: ganzrational nennt man zum Beispiel die linearen, quadratischen und kubischen Funktionen. Hier stehen Regeln und Sonderfälle zum Ableiten einer ganzrationalen Funktion. => Ganzen Artikel lesen …
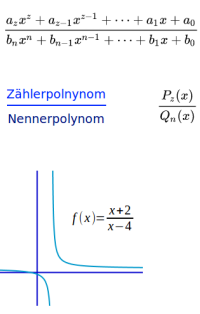
Gebrochenrationale Funktion
Definition
Im Zähler und Nenner steht jeweils eine ganzrationale Funktion: der Funktionsterm besteht aus einem Bruch. Sowohl der Zähler als auch de Nenner sind jeweils eine ganzationale Funktion (konstant, linear, quadratisch, kubisch etc.). Das Ganze nennt man dann eine gebrochenrationale Funktion. => Ganzen Artikel lesen …
