Gleichung

Definition

4x+5 = 41: Alle Terme zwischen denen ein mathematisches Gleichzeichen steht heißen Gleichung. Das Gleichzeichen besagt, dass links und rechts am Ende der gleiche Zahlenwert stehen sollte, aber nicht stehen muss. Das wird hier näher erklärt. => Ganzen Artikel lesen …

Proportionale Gleichung

Definition

a=m/x oder a=m:x ist der allgemeine Bauplan für eine porportionale Gleichung: auf einer Seite steht eine Zahl, auf der anderen Seite ein Bruch oder ein Quotient mit dem x im Nenner (unten). Das ist hier kurz definiert. => Ganzen Artikel lesen …

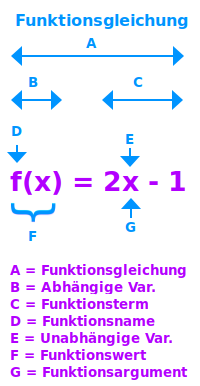
Funktionsgleichung

f(x)=Funktionsterm

f(x) = 2x-5 - Hier steht eine kurze Erklärung der Bestandteile einer Funktionsgleichung: Name, Wert, Argument, Term, unabhängige und abhängige Variable. => Ganzen Artikel lesen …

8: Eine Ganzrationale Gleichung dritten Grades lösen über Faktorisieren

… siehe unter => Kubische Gleichungen über Faktorisieren

9: Ganzrationale Gleichung 0ten Grades

… siehe unter => Konstante Gleichung

10: Ganzrationale Gleichung 1ten Grades

… siehe unter => lineare Gleichung

11: Ganzrationale Gleichung 2ten Grades

… siehe unter => quadratische Gleichung

12: Ganzrationale Gleichung 3ten Grades

… siehe unter => kubische Gleichung

13: Ganzrationale Gleichung 4ten Grades

… siehe unter => quartische Gleichung

14: Ganzrationale Gleichung 5ten Grades

… siehe unter => quintische Gleichung

16: Ganzrationale Gleichung dritten Grades

… wie etwa 0=x³-2x²+4x-3, heißt => kubische Gleichung

17: Ganzrationale Gleichung dritten Grades lösen über Faktoriseren

… siehe unter => Kubische Gleichungen über Faktorisieren

18: Ganzrationale Gleichung dritten Grades über Faktorisieren

… siehe unter => Kubische Gleichungen über Faktorisieren

19: Ganzrationale Gleichung ersten Grades

… wie 3x+4=20, heißt auch => lineare Gleichung

20: Ganzrationale Gleichung fünften Grades

… höchster Exponent von x ist 5, heißt auch => quintische Gleichung

21: Ganzrationale Gleichung nullten Grades

… ein anderes Wort für => Konstante Gleichung

22: Ganzrationale Gleichung vierten Grades

… Gleichung mit x-hoch-vier, heißt auch => quartische Gleichung

23: Ganzrationale Gleichung vom Grad drei über Faktorisieren

… siehe unter => Kubische Gleichungen über Faktorisieren

24: Ganzrationale Gleichung vom Grad null

… so etwas wie 4=4 oder 0=1, Definition unter => Konstante Gleichung

25: Ganzrationale Gleichung zweiten Grades

… wie etwa 0=x²-8x+15, heißt auch => quadratische Gleichung

26: Ganzrationale Gleichungen dritten Grades

… höchster Exponent von x ist 3 => Kubische Gleichungen

27: Ganzrationale Gleichungen dritten Grades lösen über Faktorisieren

… siehe unter => Kubische Gleichungen über Faktorisieren

28: Ganzrationale Gleichungen dritten Grades über Faktorisieren

… siehe unter => Kubische Gleichungen über Faktorisieren

29: Ganzrationale Gleichungen dritten Grades über Faktorisieren lösen

… siehe unter => Kubische Gleichungen über Faktorisieren

30: Ganzrationale Gleichungen rationale Nullstellen

… siehe unter => Satz über rationale Nullstellen

31: Ganzrationale Gleichungen über Satz über rationale Nullstellen

… siehe unter => Ganzrationale Gleichungen über Teilermethode

32: Ganzrationale Gleichungen über Taschenrechner

… lösen, geht oft über den Befehl => Polyroots