Mit Grenze
Finis ist Latein für Grenze. Finit ist im Deutschen das dazugehörige Adjektiv und heißt entsprechend: begrenzt. Der äußerste Rand des Festlandes in der Bretagne etwas heißt Kap Finisterre, wörtlich: das Kap am Ende der Welt. In der Mathematik und den Naturwissenschaften spricht man zum Beispiel von der => Finite-Elemente-Methode
… ein typischer => Plutonit
Meint so viel wie: am Ende, zuletzt, schlussendlich
Der zweite Weltktieg brachte den Tod für mindestens 50 Millionen Menschen. Der finale Schlussakt war der Abwurf von zwei Atombomben auf Städte in Japan, siehe auch => Hiroshimabombe
Das was oben ist
Man spricht zum Beispiel von einem Dachfirst. Das ist der oberste Balken, der ein Dach nach oben abschließt. First ist mit dem englischen Begriff first sowie dem deutschen Fürst verwandet: all diese Wörter teilen die Bedeutung des ersten oder obersten. => Ganzen Artikel lesen …
Ohne Grenze
Finis ist Latein für Grenze. Die Vorsilbe „in“ kehrt die Bedeutung um, sodass infinit dann für grenzenlos, unbegrenzt steht. In der Mathematik und den Naturwissenschaften bezeichnet das Wortteil infinit oft, dass ein Verfahren oder Prozess unendlich fortgesetzt werden kann. Das Gegenteil von infinit ist => finit
Programmieren
In Programmiersprachen schneidet INT oft alle Nachkommastellen ab: in vielen Programmiersprachen kann man mit INT eine Zahl damit abrunden. INT schneidet dabei einfach alle Nachkommastellen ab. Mathematisch nennt man das auch die Abrundungsfunktion. INT kommt von dem englischen Wort Integer, was auf Deutsch Ganzzahl (ganze Zahl) meint. Hier stehen einige Beispiele dazu. => Ganzen Artikel lesen …
Fit
… im Sinne der Evolutionstheorie, siehe unter => Fitness
Ad infinitum
… immer weiter so bis in alle Unendlichkeit => infiniter Regress
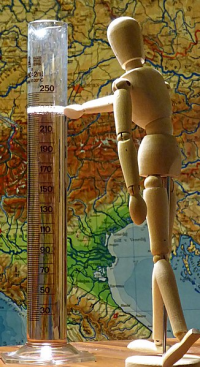Definition
≝ Genaue Beschreibung, was ein Wort meint
Laut Duden heißt definieren „den Inhalt [eines Begriffes] auseinanderlegen, erklären“ oder „bestimmen, festlegen; angeben oder beschreiben, worum es sich handelt“. Definieren ist lateinischen Ursprungs und heißt wörtlich: aus einer Grenze herleiten, begrenzen. Mit einer Definition legt man einen (möglichst) genauen Bedeutungsinhalt, auch Begriff genannt, für ein Wort oder Zeichen fest. => Ganzen Artikel lesen …
… Annäherungen unter => Leben
≝ Beispiele
Beispiele aus der Mathematik: Kreis, Kugel, Parallelogramm und so weiter. Was eine Definition ist, also eine Definition von Definition steht unter => Definition
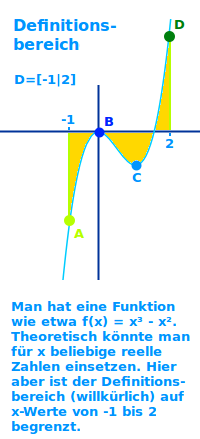Definitionsbereich
Definition
Alle Zahlen, zu denen es einen sinnvoll zuordenbaren y-Wert geben soll: das Wort Definitionsbereich wird zum Beispiel im Zusammenhang mit mathematischen Funktion, Aussagen oder Gesetzen gebraucht. Der Definitionsbereich sind alle x-Werte denen die Funktion eindeutig einen mathematisch oder sonstwie sinnvoll deutbaren y-Wert zuordnet. => Ganzen Artikel lesen …
… Abgrenzung unter => Definitionsbereich und Intervall
Erklärung im Sinne von Zuordnungen
Eine Funktion ordnet jedem Element einer Quellmenge (auch Definitionsbereich genannt) genau ein Element einer Zielmenge zu. Die Bildmenge besteht aus den Werten, die tatsächlich angenommen werden. => Ganzen Artikel lesen …
Abgrenzung und Gemeinsamkeiten
Der Definitionsbereich legt alle Zahlen fest, die man überhaupt in Betracht ziehen will oder erlaubt. Ein Intervall ist dann eine Auswahl davon, die man tatsächlich auch verwendet. Das wird hier näher erläutert. => Ganzen Artikel lesen …
Übersicht zu verschiedenen Begriffen
Die Begriffe gehören alle zu den Themen „Funktionen“ und „Gleichungen“. Die Worte unterscheiden einerseits die Zahlen, die man einsetzen darf (erlaubte x-Werte) und die rauskommen dürfen (mögliche y-Werte). Andererseits unterscheiden sie auch, was nicht nur rauskommen darf, sondern auch wirklich rauskommt (y-Werte die wirklich vorkommen). => Ganzen Artikel lesen …
Häufige aus der Schulmathematik
- => x Element der natürlichen Zahlen
Denkbare x-Werte einer Funktion, für die es keine y-Werte gibt
Eine Definitionslücke einer mathematischen Funktion ist ein x-Wert für den kein y-Wert angegeben ist. Der Definitionslücke gegenüber steht der Definitionsbereich: das sind alle x-Werte, für die auch ein y-Wert angegeben ist. Lies mehr dazu unter => Definitionslücken
Arten und Beispiele
Hebbare, Sprungstellen, Pol- und Oszillationsstellen: hier stehen einige Beispiele für mathematische Definitionslücken von Funktionen kurz erklärt. => Ganzen Artikel lesen …
… alle erlaubten x-Werte, heißt auch => Definitionsbereich
ist definiert als
Beispiel: x̄ = (a+b):2 => Ganzen Artikel lesen …
Definitionen
Ziffern rechts vom Komma nennt man Dezimale, ihre Position eine Dezimalstelle. Beides ist hier kurz auseinandergehalten. => Ganzen Artikel lesen …
Definintionen aus verschiedenen Quellen
Eine mathematische Definition sollte unter anderem dabei helfen, die folgenden Fragen mit ausschließlich ja oder nein beantworten zu können: => Ganzen Artikel lesen …
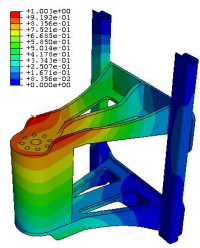Finite-Elemente-Methode
Berechnen durch endliches Zerlegen
Reale Bauteile von technischen Anlagen unterliegen oft starken Beanspruchungen: die Türme von Windkraftanlagen biegen sich im starken Sturm, die Hitzeschilde von landenden Raumfahrzeugen werden auf einige Tausend Grad Celsius erhitzt. Für die Berechnung werden die Bauteile oft in begrenzte Flächen- oder Raumelemente zerlegt: die finiten Elemente => Ganzen Artikel lesen …
… ist nicht linear, warum steht unter => senkrechte Gerade
… ist nicht linear, warum steht unter => senkrechte Gerade
… alle Spalten sind gleich, Definition unter => Grenzmatrix
Definition
f(x) = x/sin(x) hat bei x=0 eine hebbare Definitionslücke bei x=0 und y=1: der Graph einer Funktion f(x) kann durch einen hinzugefügten Punkt wieder stetig gemacht werden, wo er vorher nicht stetig war. => Ganzen Artikel lesen …
Beispiele
Als hebbar bezeichnet man eine Definitionslücke einer Funktion f(x) bei der am Graph genau ein Punkt nicht definiert ist, der aber so ergänzt werden kann, dass der Graph anschließend stetig ist. Dazu stehen hier einige Beispiele. => Ganzen Artikel lesen …
Infiniter Regress
Beispiel
Warum hat Albert Einstein die Relativitätstheorie entwickelt? Weil er sich für Physik interessierte. Warum interessiert er sich sich für Physik? Weil seine Familie ihn dazu anregete. Warum regte sein Familie ihn dazu an? Und immer so weiter bis zum Urknall und der Frage nach dem Warum unseres Seins: als infiniten Regress bezeichnet man eine Folge logischer Schlüsse oder Gedanken, die an keiner Stelle abbrechen und zu einem Endpunkt kommen. Theorien, die zu einem infiniten Regress führen, gelten in der Wissenschaft nicht als gut begründet (was aber nicht heißt, dass sie falsch sein müssen). Dazu stehen hier kurz einige Beispiele. => Ganzen Artikel lesen …
Definition
Als Infinitesimal bezeichnet man einen so kleinen Zeit- oder Raumabstand, dass dieser ohne jede praktische Bedeutung für Mess- oder Rechenvorgänge ist. Das Wort wird innerhalb der Analysis eher vermieden und durch die Idee des Grenzwertes ersetzt. Das ist hier näher erklärt. => Ganzen Artikel lesen …
Übersicht
Die Differential- und Integralrechnung sollten korrekt zusammengefasst werden zur Analysis. Die alternative Verwendung von Infinitesimalrechnung gilt heute als überholt und wird hier nicht empfohlen. Lies mehr dazu unter => Infinitesimal
Definition
In der Mathematik ist eine positive Infinitesimalzahl ein Objekt, welches bezüglich der Ordnung der reellen Zahlen größer ist als null, aber kleiner als jede noch so kleine positive reelle Zahl. Diese Definition ist hier kurz erklärt. => Ganzen Artikel lesen …
… Abgrenzung unter => Definitionsbereich und Intervall
… Abgrenzung unter => Definitionsbereich und Intervall
