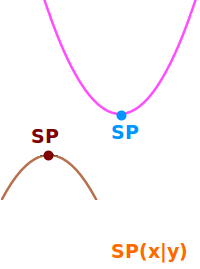
 Scheitelpunkt
Scheitelpunkt
Mathematik
Bei Funktionsgraphen ist ein Scheitelpunkt (SP) der höchste oder tiefste Punkt einer Parabel. Neben dieser Bedeutung gibt es aber auch noch weitere. => Ganzen Artikel lesen …
… von Parabeln, siehe unter => Scheitelpunkte von Parabeln
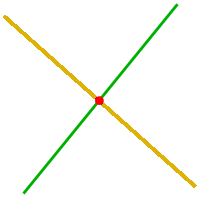 Schnittpunkt
Schnittpunkt
Definition
Ein Schnittpunkt ist ein gemeinsamer Punkt von zwei oder mehr Objekten. Ein Schnittpunkt muss also gleichzeitig zu mindestens zwei Objekten gehören. Objekte können sein: Mengen, Körper, Flächen, Linien, Geraden, Punktemengen etc. => Ganzen Artikel lesen …
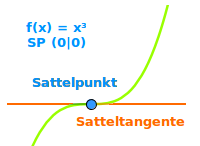 Sattelpunkt
Sattelpunkt
Wendepunkt mit waagrechter Tangente
Jeder Sattelunkt, sehr treffend auch Horizontalwendepunkt genannt, ist immer auch ein Wendepunkt: an dem Punkt wendet (ändert) sich die Krümmungsrichtung eines Graphen. Gleichzeitig ist die Steigung in dem Punkt immer gleich 0, die Wendetangente verläuft also waagrecht. Das ist hier näher erklärt. => Ganzen Artikel lesen …
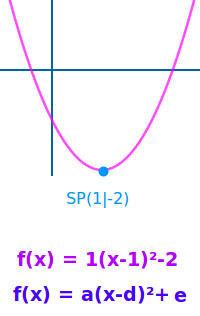 Scheitelpunktform
Scheitelpunktform
f(x) = a·(x-d)² + e
Von quadratische Funktionen und Parabeln: aus der Scheitelpunktform y oder f(x) = a·(x²-d)²+e kann man leicht den Scheitelpunkt, die Öffnung und den y-Achsenabschnitt ablesen einer Parabel in einem xy-Koordinatensystem ablesen. Umgekehrt kann man sie leicht aufstellen, wenn man von einer Parabel den Scheitelpunkt SP und irgendeinen weiteren Punkt kennt. Das ist im Folgenden beschrieben. => Ganzen Artikel lesen …
… einer Parabel, meint dasselbe wie => Scheitelpunktform
… Rechenbeispiel unter => Scheitelpunktform in Allgemeine Form
… Erklärung mit Aufgaben unter => Scheitelpunktform in Allgemeine Form
… Erklärung mit Aufgaben unter => Scheitelpunktform in Allgemeine Form
… Erklärung mit Aufgaben unter => Scheitelpunktform in Allgemeine Form
f(x) = ax²+bx+c in a·(x-d)²+e
Die allgemeine Form [1] bezieht sich hier auf quadratische Funktionen bzw. Gleichungen. Es gibt verschiedene Verfahren, sie in die Scheitelpunktform umzuwandeln. => Ganzen Artikel lesen …
Anleitung
Eine Funktion der Form f(x) = ax²+bx+c kann man immer umwandeln in die Scheitelpunktform f(x) = a·(x-d)²+e. In der Schulmathematik wird das oft mit Hilfe der quadratischen Ergänzung (QE) gemacht. Hier ist eine Alternative dazu, die für praktische Zwecke dasselbe Ergebnis liefert. => Ganzen Artikel lesen …
Anleitung
Eine quadratische Funktion in allgemeiner Form f(x)=4x²-24x+32 wird umgeformt in die Scheitelpunktform: f(x)=4·(x-3)²-4. Wie das mit Hilfe der quadratischen Ergänzung (QE) geht wird hier in kleinen Schritten erklärt. => Ganzen Artikel lesen …
… Rechenbeispiel unter => Allgemeine Form in Scheitelpunktform
… ist a(x-d)²+e, heißt einfach nur => Scheitelpunktform
… Es gibt mehrere Verfahren => Scheitelpunkt einer Parabel bestimmen
… Es gibt mehrere Verfahren => Scheitelpunkt einer Parabel bestimmen
… Es gibt mehrere Verfahren => Scheitelpunkt einer Parabel bestimmen
… Erklärung mit Aufgaben => Scheitelpunktform aus drei Punkten
… Rechenbeispiel unter => Faktorisierte Form in Scheitelpunktform
… Rechenbeispiel unter => Scheitelpunktform in faktorisierte Form
… Rechenbeispiel unter => Faktorisierte Form in Scheitelpunktform
Schritt-für-Schritt
Man hat eine Funktionsgleich in faktorisierter Form FF gegeben: f(x) = a·(x-b)(x-c). Gesucht ist die Scheitelpunktform SPF f(x) = a·(x-d)²+e. Hier wird ein Weg vorgestellt, der immer funktioniert. => Ganzen Artikel lesen …
… Rechenbeispiel unter => Faktorisierte Form in Scheitelpunktform
… Rechenbeispiel unter => Scheitelpunktform in Normalform
Umwandlung
Man hat f(x) = x²+px+q gegeben und sucht f(x) = a(x-d)²+e. Hier ist Schritt-für-Schritt erklärt, wie man das mit Hilfe der sogenannten quadratischen Ergänzung umwandelt. => Ganzen Artikel lesen …
… siehe unter => Normalform in Scheitelpunktform
… Umwandlung von quadr. Funktionen, siehe => Normalform in Scheitelpunktform
Eine quadratische Funktion für eine Parabel
Zeichnet man für eine quadratische Funktion einen Graphen, so entsteht immer eine Parabel. Zu jeder Parabel kann man eine quadratische Funktionsgleichung aufstellen, die genau diese Parabel beschreibt. => Ganzen Artikel lesen …
… siehe unter => Scheitelpunktform
Höchster oder tiefster Punkt
Der Graph einer quadratischen Funktion, zum Beispiel f(x)=x²-8x+15 hat immer einen höchsten oder einen tiefsten Punkt. Diesen Punkt nennt man den Scheitelpunkt der Parabel. Im Beispiel liegt er bei (4|-1). Bei anderen Graphen spricht man nicht von einem Scheitelpunkt. Lies mehr unter => Scheitelpunkt einer Parabel
… f(x)=Ax²+Bx+C => Scheitelpunkt aus allgemeiner Form
… f(x)=Ax²+Bx+C => Scheitelpunkt aus allgemeiner Form
… f(x)=Ax²+Bx+C => Scheitelpunkt aus allgemeiner Form
… alle Verfahren unter => Scheitelpunkt einer Parabel bestimmen

