Arten
In der Grundschulmathematik sind Reihen Abfolgen von Zahlen mit immer gleichen Zwischenschritten. Es gibt z. B. die Zweier-, Dreier-, Viererreihe und so weiter. In der höheren Mathematik nennt man so etwas eine Folge. Eine Reihe in der höheren Mathematik ist immer eine Summe (Pluskette) bei der die einzelnen Glieder nach einer festen Regeln erzeugt werden. Hierzu einige Beispiele und Arten. => Ganzen Artikel lesen …
Bedeutungen
In der Grundschule spricht man von Zahlenreihen: Zweierreihe, Dreierreihe und so weiter. In der Höheren Mathematik ist eine Reihe eine Summe einer unendlich langen Folge. Beides ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Reiher
Vogelart
Schreitvögel, die gerne am Wasser leben: Reiher kennt man aus unserer Gegend als große Vögel, die gerne in feuchten Gebieten waten und nach Futter suchen. Es gibt viele verschiedene Reiherarten. Die kleinsten sind kaum 30 Zentimeter hoch, die längsten bis zu 1,4 Meter. Reiher leben gerne nahe am Süsswasser. Auf hoher See trifft man sie nicht an. Typisch für Reiher ist der S-förmige Hals, was besonders bei fliegenden Tieren stark ausgeprägt ist. Nach dem Reiher ist auch eine Pflanze benannt, der => Reiherschnabel
… .. 🏇 kontrolliert auf Pferden sitzend sich fortbewegen, siehe auch => Pferd
Technischer Fachbegriff [Bergbau]
In der Mathematik, Physik oder Chemie: kurze Erklärung von Fachworten, Symbolen und Formeln => Ganzen Artikel lesen …
Beispiele
Eine arithmetische Reihe ist eine unendlich lang gedachte Pluskette bei der zwischen benachbarten Glieder immer der gleiche Zahlenunterschied besteht. Hier stehen Beispiele dazu. => Ganzen Artikel lesen …
… zum Üben mit der Statistik => Datenlisten
… wie z. B. 0 2 4 6 8 10 Siehe unter => Zahlenreihen
… wie z. B. 0 2 4 6 8 10 Siehe unter => Zahlenreihen
… wie z. B. 0 2 4 6 8 10 Siehe unter => Zahlenreihen
Beispiele
Es gibt endliche und unendliche Reihen, also Plusketten, das heißt Summenterme. Summenerme mit einer endlichen Anzahl von Gliedern nennt man endliche Reihen. => Ganzen Artikel lesen …
Höhere Mathematik
Bei Folgen denkt man sich Zahlen einfach aufgelistet vor. Die einzelnen Zahlen heißer Glieder. Bei arithmetischen Folgen kommt man immer mit der gleichen Addition von einer alten zum nächtsen Glied. Arithmetische Folgen hießen in der Grundschule Zahlen- oder Malreihen. Bei geometrischen Folgen kommt man immer mit der gleichen Multiplikation von einem zum nächste Glied. => Ganzen Artikel lesen …
Anleitung
Die Drei hat als Vielfache die Zahlen: 0, 3, 6, 9, 12, 15 und so weiter. Die Vier hat als Vielfache die Zahlen: 0, 4, 8, 12, 16 und so weiter. Die kleinste Zahl, die von beiden ein Vielfaches ist, ist hier die 12. Man schreibt: kgV(3;4)=12. Das Verfahren zur Bestimmung über Zahlenreihen ist hier Schritt-für-Schritt erklärt. => Ganzen Artikel lesen …
Beispiele
Maclaurin-Reihen sind ein Sonderfall der Taylorreihen. Insbesondere in der Ingenieurmathematik werden sie häufig zur Berechnung von Näherungswerten verwendet. Hier stehen einige Beispiele. => Ganzen Artikel lesen …
… Meint meistens: die Zahlenreihen für das Einmaleins, siehe auch => Zahlenreihen
Kombinatorik
Wenn 1;2;3 dasselbe ist wie 3;2;1 spricht man von einer Variation. Die Reihenfolge spielt also eine Rolle, man sagt kurz: mit Reihenfolge. Wenn 1;2;3 dasselbe sein soll wie 3;2;1 - das heißt nur einmal gezählt wird - dann spricht man von einer Kombination. Zwei Anordnungen mit unterschiedlicher Reihenfolge können gleich sein. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Kombinatorik
Wichtig ist nur, was man hat, nicht in welche Reihenfolge: 1;2;3 wäre damit gleich 2;3;1. Die Unterscheidung spielt in der Kombinatorik, der Statistik und der Stochastik eine wichtige Rolle. => Ganzen Artikel lesen …
Beispiele
Maclaurin- und Taylor-Reihe sind die zwei klassischen Anwendungsfälle von Potenzreihen. Sie spielen eine große Rolle, zum Beispiel in den Ingenieurwissenschaften. Eine Übersicht steht unter => Potenzreihe [Hauptseite]
Mathematik
Grundsätzlich rechnet man von links nach rechts. Aber mal und geteilt rechnet man immer vor plus und minus. Und Hoch (Potenzen) ist noch stärker als mal und geteilt. Am stärksten wirken Klammern. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
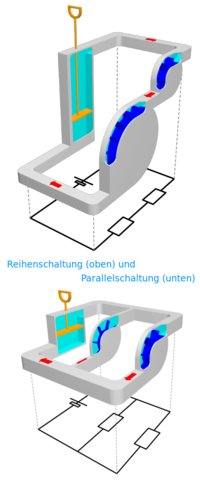Reihen- und Parallelschaltung
Vergleich
Elektrischen Strom kann man sich aus Stromteilchen vorstellen, die durch eine elektrische Leitung fließen. Die Teilchen fließen dabei gemeinsam in derselben Richtung. Führt das Ende der Leitung wieder zum Anfang der Leitung zurück, spricht man von einem Stromkreis. Teilt man die Leitung unterwegs in mehrere nebeneinander laufende Leitung auf, entsteht aus der Reihenschaltung eine Parallelschaltung. Das wird hier weiter erklärt. => Ganzen Artikel lesen …
… wie z. B. 0 2 4 6 8 10 Siehe unter => Zahlenreihen
… wie z. B. 0 2 4 6 8 10 Siehe unter => Zahlenreihen
… wie z. B. 0 2 4 6 8 10 Siehe unter => Zahlenreihen
… Nummerierung der Glieder einer Reihe, meist unten rechts klein geschrieben, siehe auch => Reihe
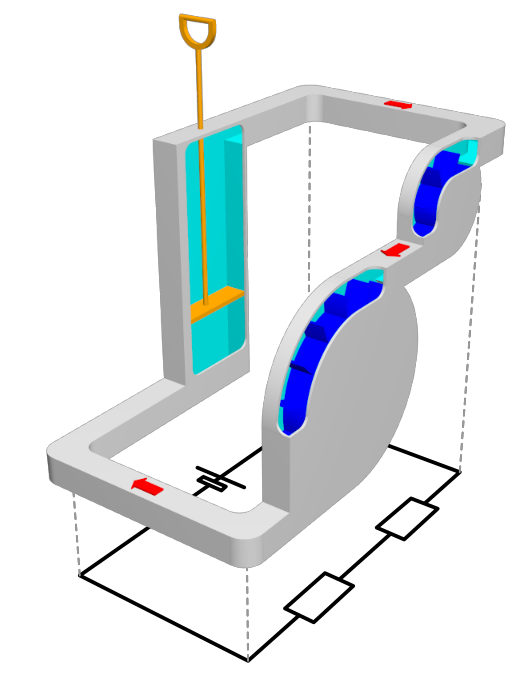Reihenschaltung
Strom
Elektrischen Strom kann man sich aus Stromteilchen vorstellen, die durch eine elektrische Leitung fließen. Die Teilchen fließen dabei gemeinsam in derselben Richtung. Führt das Ende der Leitung wieder zum Anfang der Leitung zurück, spricht man von einem Stromkreis. Der einfachste Fall ist die Reihenschaltung. => Ganzen Artikel lesen …
Elektrik
Hat man mehrere elektrische Widerstände in Reihe geschaltet, kann man ihre Ohm-Zahlen direkt addieren. Das Ergebnis ist dann der Gesamtwiderstand. Schwieriger zu berechnen ist die => Parallelschaltung von Widerständen
Energetische Sanierung
Exemplarische Rechnung für ein kleinen Reihenendhaus nahe der Stadt Aachen. Die zentrale Frage ist: welche Energiemenge nach Wärme und Strom unterschieden kann realistischerweise pro Jahr erzeugt werden. => Ganzen Artikel lesen …
… Beispiele, siehe unter => Maclaurin-Reihen
… Summen mit einer unendlich großen Anzahl von Summanden (Gliedern), Definition unter => Reihe
Listen
Einer-, Zweier-, Dreierreihe etc. Hier stehen Beispiele aus der Grundschule dazu. In der höheren Mathematik steht das Wort Reihe für eine lange Pluskette (Summe), bei der die einzelnen Summanden meist durch eine knapp angegebene Regel erstellt werden können. => Ganzen Artikel lesen …
… wie z. B. 0 2 4 6 8 10 Siehe unter => Zahlenreihen
Aufgaben
Man hat den Anfang und das Ende einer Zahlenfolge gegeben. Beispiel: 28, 30, 32 48. Dazwischen sind Leerfelder gelassen. Diese soll man ausfüllen. => Ganzen Artikel lesen …
Physik
Praktisch und historisch wichtig sind die Zerfallsreihen der drei primordialen Radionuklide Uran-238, Uran-235 und Thorium-232, auch Natürlich radioaktive Familien genannt. Sie entstehen durch Alpha- und Beta-Zerfälle, die mehr oder weniger regelmäßig abwechselnd aufeinander folgen. (Manche der beteiligten Nuklide haben auch die alternativ mögliche, aber seltene Zerfallsart Spontanspaltung; sie führt aus der jeweiligen Zerfallsreihe hinaus und wird hier nicht beachtet). => Ganzen Artikel lesen …
