 Radius
Radius
Mathematisch
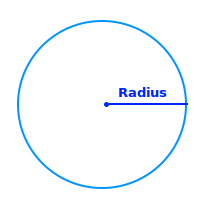
Der Radius ist die Strecke von der Mitte eines rundlichen Gebildes bis zum Rand. Die übliche Abkürzung ist ein kleines r oder ein großes R. => Ganzen Artikel lesen …
Chemie
Radium ist ein stark radioaktives chemisches Element mit dem Elementsymbol Ra und der Ordnungszahl 88 aus der Gruppe der Erdalkalimetalle (2. Hauptgruppe im Periodensystem). Reines Radium ist hell-bläulichweiß glänzend, reagiert heftig mit Wasser und Säuren und färbt die Flamme intensiv rot. => Ganzen Artikel lesen …
Kreis
Radial heißt so viel wie: auf einer geraden Linie, die durch die Mitte eines Kreises geht. Hier stehen einige Beispiele dazu. => Ganzen Artikel lesen …
Beispiele
Erdradius, Kegelradius oder Bohrscher Radius: der Rad ist der Abstand von einer Kugel- oder Kreismitte bis zum Rand der Kugel oder des Kreises. Hier steht eine Liste mit Beispielen. => Ganzen Artikel lesen …
… falsche Mehrzahl von Radius, richtig ist => Radien
6357 Kilometer
Der Radius der Erde ist die Strecke vom Erdmittelpunkt bis zur Erdoberfläche. Diese Strecke ist nicht für alle Punkte der Erdoberfläche gleich. Am Äquator ist der Erdradius etwas größer (6378 km). Siehe auch => Erdradius
… Radius von der Erdmitte bis irgendwo zum Äquator: 6378 Kilometer => Erdradius
… die Hälfte des => Atomkerndurchmesser
 Atomradius
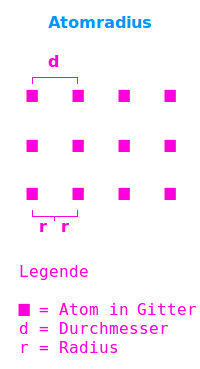
Atomradius
Vom Kern zur Atomhülle
Zum Beispiel 25 Pikometer (pm) für Wasserstoff: als Atomradius bezeichnet man die Strecke von der Mitte eines kugelig gedachten Atom bis zum äußersten Elektron oder alternativ: die Hälfte des Abstandes zwischen den Mittelpunkten regelmäßig angeordneter Atome. => Ganzen Artikel lesen …
… Liste aller Atomradien => Atomradien
 Außenradius
Außenradius
Von der Mitte bis zum äußeren Ende der Hülle, des Randes
Das Wort Radius gehört zu Kreisen und Kugeln. Bei Kreisen und Kugeln meint der Radius an sich immer die Strecke von der Mitte bis zum Rand. Dabei denkt man sich den Rand als extrem dünne Linie (Kreis) oder eine extrem dünne Hülle (Kugel). Das Wort Außenradius kommt ins Spiel, wenn der Rand nicht mehr extrem dünn sondern irgendwie breit ist. Dann gibt es sozusagen einen eigenen Radius für den inneren Rand und einen anderen größeren Radius für den äußeren Rand. Den Radius für den äußeren Rand nennt man Außenradius. => Ganzen Artikel lesen …
 Bahnradius
Bahnradius
r
Von einem Bahnradius r spricht man bei einer Kreisbewegung. So bewegt sich etwas der Mond in etwa auf einer Kreislinie um die Erde. Der Abstand des Mondmittelpunktes zum Erdmittelpunkt wäre dann ein Bahnradius. Der Bahnradius spielt eine wichtige Rolle bei vielen Berechnungen zur => Kreisbewegung
 Bodenradius
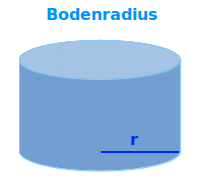
Bodenradius
Geometrie
Pyramiden, Würfel, Zylinder oder Kegel: Körper haben oft einen Boden. Das ist die Fläche, auf der sie stehen. Oft ist der Boden ein Kreis. Bei Kreisen spricht man von einem Radius. Das ist die Strecke von der Mitte bis zum Rand. Diese Strecke ist dann der Bodenradius. Die übliche Abkürzung ist ein kleines r. Siehe auch => Radius
Physik
0,5291772106 mal 10 hoch minus 10 Meter: der Bohrsche Radius, oft mit a und kleinem Index 0 abgekürzt, bezeichnet den Radius des Wasserstoffatoms im niedrigsten Energiezustand und somit auch den Radius seiner ersten und kleinsten Elektronenschale im Rahmen des Bohrschen Atommodells; dabei bleibt die kleine Korrektur noch unberücksichtigt, die der Mitbewegung des Atomkerns um den Schwerpunkt entspricht. => Ganzen Artikel lesen …
Physik
Zurzeit (2020) ist es unklar, ob ein Elektron überhaupt eine Ausdehnung, also eine Größe hat. Es ist möglich, dass es eine mathematische Punktmasse ist und somit unendlich klein ist. Mehr dazu unter => Elektronendurchmesser
 Erdradius
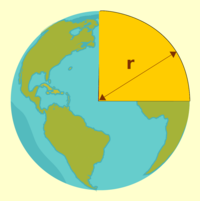
Erdradius
6371 km
Der Radius der Erde ist die Strecke vom Erdmittelpunkt bis zur Erdoberfläche. Da die Erde keine ganz perfekte Kugel ist, kann man unterschiedliche Radien angeben. Üblich sind der Pol- und und der Äquatorradius. => Ganzen Artikel lesen …
… A = pi mal Siehe unter => Kreisfläche aus Kreisradius
… A = pi mal Siehe unter => Kreisfläche aus Kreisradius
Geometrie
Zylinder und Kegel haben als Grundfläche einen Kreis. Der Radius dieses Kreises ist der Grundkreisradius. Der Radius ist immer die Strecke von der Mitte eines Kreises bis zum Rand eines Kreises. Die beiden Fälle Zylinder und Kegel sind hier kurz vorgestellt. => Ganzen Artikel lesen …
 Innenradius
Innenradius
Von der Mitte bis zum Anfang der Hülle, des Randes
Der Innenradius, oft abgekürzt mit einem kleinen r, ist der Abstand von der Mitte bis zum inneren Rand eines Randes oder einer Hülle. => Ganzen Artikel lesen …
… 231 mal 10 hoch -12 Meter, siehe auch => Atomradius
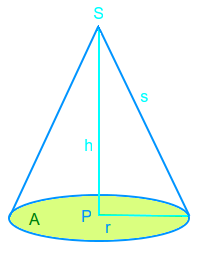 Kegelradius
Kegelradius
r: Radius der kreisförmigen Grundfläche
Ein Kegel hat immer einen kreisförmigen Boden (Grundfläche). Dieser Kreis hat einen Radius: das ist die Strecke von der Mitte bis zum Kreisrand. Dieser Kreisradius heißt bei einem Kegel auch Kegelradius. => Ganzen Artikel lesen …
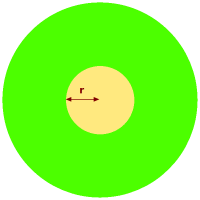 Kernradius
Kernradius
Physik
In der Atomphysik spricht man von Atomkerndurchmesser (10 hoch -15 bis 10 hoch -14 m). In der Geophysik gibt es den Erdkerndurchmesser (6942 km). Beides ist hier kurz vorgestellt. => Ganzen Artikel lesen …
 Konvergenzradius
Konvergenzradius
Definition
Die Potenzreihe x^n - sprich: x hoch n - hat einen Konvergenzradius von 1. Das wird hier Schritt-für-Schritt erklärt. => Ganzen Artikel lesen …
Anleitung
Ein Konvergenzradius kann für eine Potenzreihe berechnet werden. => Ganzen Artikel lesen …
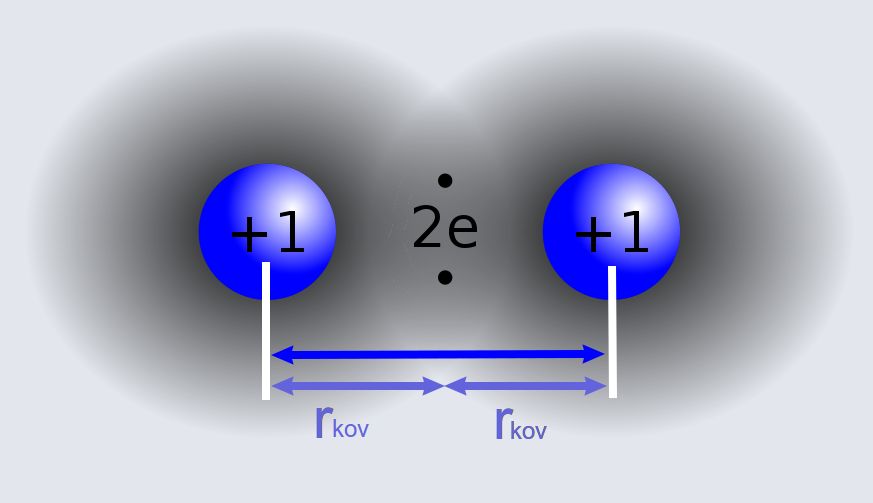 Kovalenter Radius
Kovalenter Radius
Chemie
Der Kovalente Radius bezeichnet den halben Abstand zweier Atome desselben chemischen Elements, die kovalent gebunden sind. Diese Radien hängen auch von der Art der Bindung (Einfach-, Doppel- oder Dreifachbindung) ab sowie von der Elektronegativität bei unterschiedlichen Bindungspartnern. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
… in der Chemie, üblich ist => kovalenter Radius
Radius mal 2 gibt Durchmesser
Radius mal 2 gibt Durchmesser: Wenn ein Kreis einen Radius von 4 Zentimeter hat, dann ist sein Durchmesser 8 Zentimeter. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
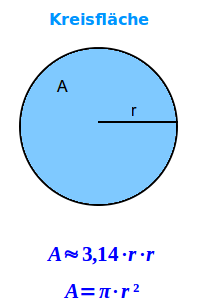 Kreisfläche aus Kreisradius
Kreisfläche aus Kreisradius
A = π·r²
Die Kreisfläche, auch Kreisflächeninhalt genannt und zum Beispiel in Quadratzentimetern (cm²) oder Quadratmetern (m²) angegeben, ist gleich der Kreiszahl pi (etwa 3,14) multipliziert mit dem Quadrat des Radiusses. Das ist hier kurz vorgerechnet. => Ganzen Artikel lesen …
… A = pi mal Siehe unter => Kreisfläche aus Kreisradius
… A = pi mal => Kreisfläche aus Kreisradius
… A = pi mal Siehe unter => Kreisfläche aus Kreisradius
 Kreisradius
Kreisradius
Die Strecke von der Kreismitte bis zum Rand des Kreises
Die gerade Strecke von der Kreismitte bis zu irgendeinem beliebigen Punkt auf dem Rand eines Kreises nennt man den Kreisradius. Die übliche Abkürzung ist ein kleines lateinisches r. Der Kreisradius ist immer halb so lang wie der => Kreisdurchmesser
Durchmesser geteilt durch 2 gibt Kreisradius
Durchmesser d geteilt durch 2 gibt Kreisradius r. Wenn ein Kreis einen Durchmesser von 20 Zentimetern hat, dann ist sein Radius genau 10 Zentimeter. Siehe auch => Kreisradius berechnen
==== Formel ====
r = Wurzel aus (A:pi) oder kurz auch r = √(A/π) sind zwei Varianten derselben Formel. Damit kann man direkt und ohne Umformungen den Radius eines Kreises berechnen, wenn man den Flächeninhalt kennt. Hier steht die Formel mit Legende. => Ganzen Artikel lesen …

