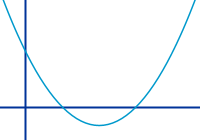
Quadratische Funktion
f(x)=ax²+bx+c
Jede Funktion deren Gleichung man auf die Form f(x)=ax²+bx+c bringen kann heißt quadratisch. Das a darf irgendeine Zahl außer der Null sein. b und c dürfen auch - müssen aber nicht - Null sein. Der dazugehörige Graph ist immer eine (quadratische) Parabel. => Ganzen Artikel lesen …
Funktion
f(x)
f(x)=4x+8 ist eine typische mathematische Funktion: man kann für x eine beliebige Zahl einsetzen. Die Rechnung gibt dann einen y-Wert als Ergebnis der eindeutig dem eingesetzten x-Wert zugeordnet ist. Das ist die Grundidee einer Funktion. Der Gedanke wird hier ausführlich erklärt. => Ganzen Artikel lesen …
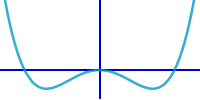Biquadratische Funktion
f(x) = ax^4 + bx^2 + c
Eine Funktion mit x hoch 4 und x hoch 2 nennt man biquadratisch. Diese Funktion und ihre Berechnungen werden hier kurz vorgestellt. => Ganzen Artikel lesen …
Arten
Reinquadratisch, gemischtquadratisch, Scheitelpunkt- oder die Normalform: hier steht eine Übersicht der am häufigsten verwendeten Darstellungsformen quadratischer Funktionen. => Ganzen Artikel lesen …
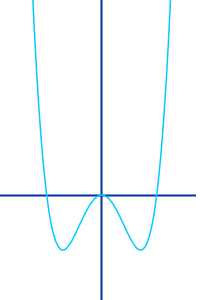Quartische Funktion
f(x)=T(x⁴)
Ganzrationale Funktion mit höchstens x hoch 4: als quartisch bezeichnet man eine Funktion, die man in die Form f(x) = a·x⁴ + b·x³ + c·x^2 + d·x + e bringen kann. Ein anderer, gleichbedeutender Name ist ganzrationale Funktion vierten Grades. Das Wort quartisch steht für 4 und bezeichnet die höchste vorkommende Potenz der unabhängigen Variablen x. => Ganzen Artikel lesen …
… von Parabeln und quadratischen Funktionen, siehe unter => Nullstellen über ABC-Formel
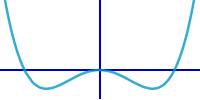Biquadratische Funktion ableiten
Zum Beispiel f(x) = 2x^4-5x^2+6 ableiten gibt f'(x) = 8x³-10x
Als biquadratisch Funktion bezeichnet man eine ganzrationale Funktion vierten grades (quartische Funktion) mit ausschließlich geraden Exponenten von x. Eine biquadratische Funktion hat die allgemeine Form f(x) = ax^4 + bx^2 + c. Durch Umformung kann man jede biquadratische Funktion in diese Form bringen. Sie kann dann mit Hilfe der Faktor- und der Potenzregel abgeleitet werden. => Ganzen Artikel lesen …
Beispiele
f(x) = 2x⁴ - 8x² + 16 - bei einer biquadratischen Funktion gibt es im Funktionsterm ein x⁴ sowie immer auch ein x². Daneben kann es - muss aber nicht - noch ein absolutes Glied geben, das heißt eine Zahl ohne x. Hier stehen einige Beispiele. => Ganzen Artikel lesen …
… siehe unter => Quadratische Funktionen Diskussion
… siehe unter => Graph aus Parabelgleichung
… so etwa wie f(x)=ax² heißt => Potenzfunktion zweiten Grades
f(x) = ax²+bx+c oder ax²+bx
Es gibt ein Glied mit x² und mit x, erlaubt ist auch eine Zahl ohne x (muss aber nicht). Entsprechende Funktionen nennt man gemischtquadratisch. => Ganzen Artikel lesen …
… siehe => Nullstellen von gemischtquadratischen Funktionen
… siehe => Nullstellen von gemischtquadratischen Funktionen
… siehe => Nullstellen von gemischtquadratischen Funktionen bestimmen
… siehe => Nullstellen von gemischtquadratischen Funktionen bestimmen
… siehe => Nullstellen von gemischtquadratischen Funktionen bestimmen
… siehe => Nullstellen von gemischtquadratischen Funktionen
… siehe => Nullstellen von gemischtquadratischen Funktionen
… siehe => Nullstellen von gemischtquadratischen Funktionen bestimmen
… siehe => Nullstellen von gemischtquadratischen Funktionen bestimmen
… siehe => Nullstellen von gemischtquadratischen Funktionen bestimmen
Definition
f(x) = ax² + bx: jede Funktion, die man in die Form f(x) = ax² + bx bringen kann heißt gemischtquadratisch ohne absolutes Glied. Gemischtquadratische meint, dass die unahbängige Variable x sowohl in einem quadratischen (ax²) als auch in einem linearen (bx) Glied vorkommt. Als absolutes Glied bezeichnet man eine Zahl ohne die unabhägige Variable x. Ein solches darf nicht vorkommen. Das ist hier näher erklärt. => Ganzen Artikel lesen …
Beispiele
Gemischtquadratisch nennt man eine quadratische Funktion bei der im Funktionsterm neben dem quadratischen Glied mit x² auch noch ein lineare Term mit x vorkommt. Hier stehen Beispiele dazu. => Ganzen Artikel lesen …
… siehe => Nullstellen von gemischtquadratischen Funktionen
… siehe => Nullstellen von gemischtquadratischen Funktionen
… siehe => Nullstellen von gemischtquadratischen Funktionen bestimmen
… siehe => Nullstellen von gemischtquadratischen Funktionen bestimmen
… siehe => Nullstellen von gemischtquadratischen Funktionen bestimmen
… siehe => Nullstellen von gemischtquadratischen Funktionen
… siehe => Nullstellen von gemischtquadratischen Funktionen bestimmen
… siehe => Nullstellen von gemischtquadratischen Funktionen bestimmen
… siehe => Nullstellen von gemischtquadratischen Funktionen bestimmen
… Graph gegeben, f(x)= oder y= gesucht => Parabelgleichung aus Graph
… siehe unter => Graph aus Parabelgleichung
