ℜ
Physik Chemie Grundschule Mathematik I Mathematik II Wissen
Kurze Worte Worte nach Alter Terme Rechner
Mathfeed Physfeed Philfeed
Das Lexikon Die Mission Die Autoren Copyright Impressum
Physik Nachhhilfe 5-10 Physik Nachhilfe 11-13 Chemie Nachhilfe 5-13 Mathe Nachhilfe 5-8 Mathe Nachhilfe 9-10 Mathe Nachhilfe 10-13
☰
1: Nähe

Beispiel

Als Nähe bezeichnet man, dass Dinge zueinander wenig Abstand haben: In der Nähe des Äquators herrschen oft ganzjährig hohe Temperaturen. Siehe als Beispiel => äquatornah
2: Ähre

Unverzweigter Blütenstand, oft mit Grannen

Eine Ähre ist ein unverzweigter Blütenstand mit einer gestreckten Hauptachse, der Ährenspindel. Ist diese Hauptachse fleischig verdickt, spricht man von einem Kolben. Die Einzelblüten sitzen bei einer Ähre ungestielt an der Spindel. Bei den meisten Ähren blühen die untersten Blüten als erste auf. Manche - nicht alle - Ähren haben lange borstenartige Fortsätze, die sogenannten Grannen. An ihrer Länge kann man (in etwa) Getreidarten wie Weizen (keine Grannen), Roggen (kurz, unterschiedlich lang) und Gerste (lang) unterscheiden. => Ganzen Artikel lesen …
3: Bache

… ein Haus- oder Wildschwein als Muttertier, ein weibliches Schwein an sich heißt => Sau
4: Bäche

Beispiele

Bäche als kleinere Wasserläufe: hier stehen einige wenige Beispiele. => Ganzen Artikel lesen …
5: Polnähe

Näher an den Polen als am Äquator

Polnah meint, dass etwas eher näher an den geographschen Polen der Erdkugel liegt als am Äquator. Das Wort nah lässt dabei offen, wie nah genau. Man kann es auf den jeweiligen Zusammenhang anpassen. => Ganzen Artikel lesen …
6: nächste

ist so richtig geschrieben.
7: Annähernd

… meint so viel ungefähr, in etwa, grob => fast
8: e angenähert

… Näherungsformeln für die Eulersche Zahl unter => e annähern
9: e annähern

Näherungsverfahren für 2,71…

e ist die Eulersche Zahl, etwa 2,718. Die Nachkommstellen setzen sich unendlich fort ohne je dabe ein erkennbares Muster zur erzeugen. Hier werden kurz Methoden zur schrittweisen Berechnung beliebig vieler Nachkommastellen vorgestellt. => Ganzen Artikel lesen …
10: e elementar annähern

… Näherungsformeln für die Eulersche Zahl unter => e annähern
11: e näherungsweise

… Näherungsformeln für die Eulersche Zahl unter => e annähern
12: Eulersche Zahl als Näherungswert

… Näherungsformeln für die Eulersche Zahl unter => e annähern
13: Eulersche Zahl annähern

… Näherungsformeln für die Eulersche Zahl unter => e annähern
14: Eulersche Zahl näherungsweise

… Näherungsformeln für die Eulersche Zahl unter => e annähern
15: Eulerzahl angenähert

… Näherungsformeln für die Eulersche Zahl unter => e annähern
16: Eulerzahl näherungsweise

… Näherungsformeln für die Eulersche Zahl unter => e annähern
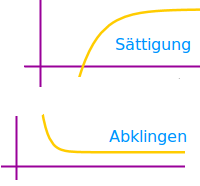17: Exponentielle Annäherung

Definition

Wenn x größer wird, gehen die Funktionswert immer näher an einen oberen Maximal- oder unteren Minimalwert heran. Praktische Beispiele sind etwa die betriebswirtschaftliche Marktsättigung (oben) oder die Abkühlung von einem Teeglas (unten). Beides ist hier kurz mathematisch benannt. => Ganzen Artikel lesen …
18: Heronsches Näherungsverfahren

… Schritt-für-Schritt Anleitung unter => Heron-Verfahren
19: Näherung e

… Näherungsformeln für die Eulersche Zahl unter => e annähern
20: Näherung für e

… Näherungsformeln für die Eulersche Zahl unter => e annähern
21: Näherungsformel e

… Näherungsformeln für die Eulersche Zahl unter => e annähern
22: Näherungsformel für e

… Näherungsformeln für die Eulersche Zahl unter => e annähern
23: Näherungsformel von Ramanujan

… berechnet in etwa den => Elllipsenumfang
24: Näherungsformeln

… für Beispiele siehe unter => Näherungsverfahren
25: Näherungslösung

60:x = 11

Man kann die Gleichung oben durch probieren immer besser lösen. Das Ergebnis eines schrittweisen Herantastens an eine Lösung nennt man eine Näherungslösung oder auch einen Näherungswert. Die Methode nennt man auch Approximation oder => Näherungsverfahren
26: Näherungsverfahren

Definition | Beispiele

Ein Näherungsverfahren, auch Approximation genannt, ist eine schrittweise Berechnung wobei mit jedem Berechnungsschritt das Ergebnis genauer erfasst wird. Hier stehe eine Liste solcher Verfahren. => Ganzen Artikel lesen …
27: Näherungsverfahren nach Heron

… Schritt-für-Schritt Anleitung unter => Heron-Verfahren
28: Näherungsweise

Ungefähr

Näherungsweise meint, dass man nicht zwingend das exakte „echte“ Ergebnis kennen will (oder kann). Vielmehr genügt es (oder es muss genügen), dann man eine ungefähre Lösung kennt. Diese ungefähre Lösung berechnet man dann in mehreren kleinen Schritten, man nähert sich der Lösung an. Das Ergebnis ist der => Näherungswert
29: Näherungsweise aber nicht exakt gleich

… ≆ meint: bis auf einen tolertierten Restfehler gleich, aber nicht genau => gleich
30: Näherungsweise gleich

… ≅ meint: bis auf einen möglichen und tolerierten Restfehler => gleich
31: Näherungswert

Mathematik

Ein Ergebnis, das in etwas stimmt, aber nicht genau sein muss: einen Näherungswert berechnet man durch schrittweise Annäherung an das wahr Ergebnis. Der Näherungswert kann, muss aber nicht, identisch sein mit dem wahren Wert. => Ganzen Artikel lesen …
32: Näherungswert für Eulersche Zahl

… Näherungsformeln für die Eulersche Zahl unter => e annähern
33: Näherungszeichen

… ≈ siehe unter => fast gleich
34: Pi annähern

… numerisch, siehe unter => Pi-Generator
35: Tiergröße und Polnähe

Je näher am Pol, desto größer

Siehe auch => Ganzen Artikel lesen …
Zur Startseite von Rhetos
Startseite
Impressum
© 2010-2023


Startseite Impressum Feedback © 2010-2023