Näherungsverfahren
Definition | Beispiele
Basiswissen
Ein Näherungsverfahren, auch Approximation genannt, ist eine schrittweise Berechnung wobei mit jedem Berechnungsschritt das Ergebnis genauer erfasst wird. Hier stehe eine Liste solcher Verfahren.
Abgrenzung
Nicht jedes schrittweise Verfahren ist ein Näherungsverfahren. Bei Näherungsverfahren kommen schon die Zwischenergebnisse immer näher an das Endergebnis heran. Ein Verfahren, das nicht zwangsweise immer genauere Zwischenergebnisse produziert nennt man einen => Algorithmus
Beispiel: Dividieren
- Das Ergebnis der Division 111:7 kann schrittweise berechnet werden.
- Bei der schriftlichen Division bringt jeder Schritt eine weitere Nachkommastelle.
- Lies mehr unter => Schriftlich dividieren
Beispiel: Wurzeln ziehen (Heron)
- Wurzeln sind oft irrationale Zahlen mit unendlich vielen Nachkommastellen.
- Zur Näherungsweisen Berechnung gibt es das => Heron-Verfahren
Beispiel: die Eulersche Zahl 2,718...
- e ist die Eulersche Zahl, etwa 2,718.
- Sie wird über bestimmte Funktionen angenähert.
- Lies mehr unter => e annähern
Beispiel: die Kreiszahl Pi
- Pi ist die sogenannte Kreiszahl, etwa 3,14.
- Sie kann über einen (sehr langen) Term angenähert werden.
- Siehe auch => Pi-Generator
Beispiel: Tangentensteigung, Punktsteigung
- In der Differentialrechnung wird die Ableitung oft näherungsweise berechnet.
- Ein üblicher Name ist h-Methode oder => Sekantenverfahren
Beispiel: Fläche von Graph
- In der Integralrechnung werden Flächen näherungsweise bestimmt.
- Lies mehr dazu unter => Säulenmethode
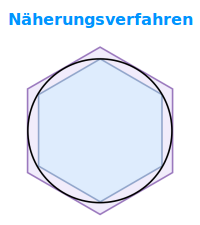
Beispiel: Kreisfläche
- Die Kreisfläche und der Kreisumfang können über Vielecke angenähert werden.
- Lies mehr dazu unter => Polygonkreis
Beispiel: Iteration/Rekursion
- Das sind Verfahren, bei denen das Ergebnis selbst als Eingabe für den nächsten Schritt gilt.
- Lies mehr dazu unter => Iteration oder Rekursion
Beispiel 2D- und 3D-Figuren
- Viele Flächen- und Körperfiguren kann man in einfachere Gebilde zerlegen.
- Zerlegt man Figuren mit krummen Grenzen in vielecke Figuren, treten Fehlreu auf.
- Je feiner aber die Zerlegung ist, desto geringer werden die Fehler.
- Beispiel: ein Kreis wird über n-Eck mit sehr großem n angenähert.
- Allgemein spricht man hier von der => Exhaustionsmethode
