 Matrix
Matrix
Mathematik
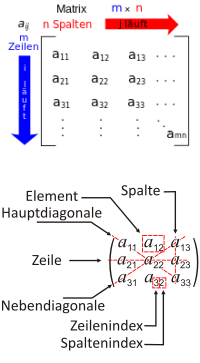
Kurzdefinition: eine Matrix ist eine tabellartige Anordnung von Elementen, meist von Zahlen. Mit Matrizen kann man dann verschiedene Rechnungen durchführen [1], so als sei die ganze Matrix eine Zahl. => Ganzen Artikel lesen …
… Matrizen ist die Mehrzahl einer => Matrix
… botanisches Fachwort für den Baum => Lärche
… ist (2020) die Hauptstadt des Landes => Spanien_
… als stochastische Matrix dasselbe wie die => Grenzmatrix
Verschiedene Bedeutungen im Sinne von Gußform
Druckereiwesen: eine Form zum Guss von Einzelbuchstaben => Ganzen Artikel lesen …
 2-mal-2-Matrix
2-mal-2-Matrix
Hat immer zwei Zeilen und zwei Spalten
Eine 2-mal-2-Matrix => Ganzen Artikel lesen …
 2-mal-2-Matrix invertieren
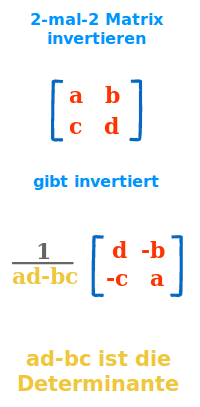
2-mal-2-Matrix invertieren
Anleitung
Die Matrix hoch minus eins gerechnet: das Invertieren von Matrizen ist sehr rechenaufwändig. Bei einer kleinen 2-mal-2 Matrix ist dies aber noch gut von Hand möglich. Das Verfahren ist hier kurz erklärt. => Ganzen Artikel lesen …
 2-mal-3-Matrix
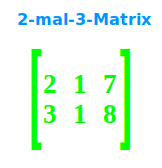
2-mal-3-Matrix
… hat 2 Zeilen und 3 Spalten, siehe auch => Matrizen
 2-mal-4-Matrix
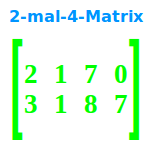
2-mal-4-Matrix
… hat 2 Zeilen und 4 Spalten, siehe auch => Matrizen
 3-mal-2-Matrix
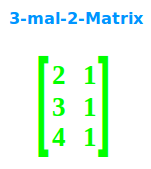
3-mal-2-Matrix
… hat 3 Zeilen und 2 Spalten, siehe auch => Matrizen
 3-mal-3-Matrix
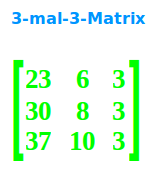
3-mal-3-Matrix
… hat 3 Zeilen und 3 Spalten, siehe auch => Matrizen
 4-mal-2-Matrix
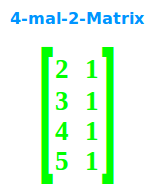
4-mal-2-Matrix
… hat 4 Zeilen und 2 Spalten, siehe auch => Matrizen
Aᴴ
Adjungiert oder auch transponiert-konjugiert nennt man eine Matrix, „die aus einer (n × n)-Matrix A = (aᵢⱼ) über ℝ oder ℂ durch Vertauschen von Zeilen und Spalten und anschließende komplexe Konjugation entstandene (n × n)-Matrix [1]“. Diese Definition ist hier kurz vorgestellt. => Ganzen Artikel lesen …
… siehe unter => schiefsymmetrische Matrix
 Bedarfsmatrix
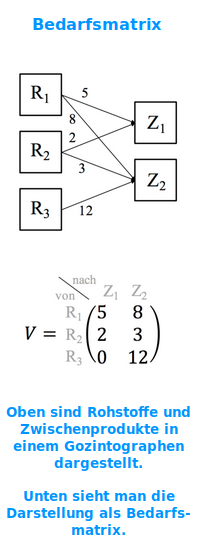
Bedarfsmatrix
Produktionsprozesse
Eine Bedarfsmatrix, auch Verflechtungsmatrix genannt, fasst Wissen tabellarisch zusammen: wie viele Mengeneinheiten bestimmter Rohstoffe benötigt man zur Produktion bestimmter End- oder Zwischenprodukte? => Ganzen Artikel lesen …
Mathematik
Eine Blockmatrix ist eine Matrix, die man in weitere sogenannte Teilmatrizen aufgeteilt hat. Wie man die Matrix dabei aufgeteilt ist nicht wichtig. Jede Matrix mit mehr als einem Element kann zu einer Blockmatrix machen. Siehe auch => Matrix
 Diagonalmatrix
Diagonalmatrix
Physik
Als Diagonalmatrix bezeichnet man eine Matrix, bei der alle Einträge außerhalb der Hauptdiagonalen Null sind. Die Hauptdiagonale geht von oben links nach unten rechts. => Ganzen Artikel lesen …
 Drehmatrix
Drehmatrix
Geometrie
In einem 2D-Koordinatensystem, auch als euklidische Ebene ℝ² bezeichnet, kann man einen Ortsvektor mit Hilfe einer Matrix über eine einfache Rechnung um einen gewünschten Winkel α um den Koordinatenursprung (0|0) gegen den Uhrzeigersinn drehen. Man spricht von einer Vektordrehung oder einer Vektorrotation. Die Lösungsidee dazu ist die sogenannte Drehmatrix, oft bezeichnet als R mit einem rechts tiefgestellten kleinen Alpha. Hier ist der Rechenweg in Worten und mit Zahlenbeispielen erklärt. => Ganzen Artikel lesen …
 Einheitsmatrix
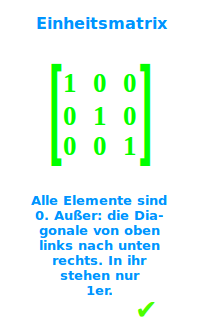
Einheitsmatrix
𝟙
Alle Elemente einer sogenannten Einheitsmatrix sind Nullen. Nur in der Hauptdiagonalen, die Diagonale von oben links nach unten rechts) stehen keine Nullen sondern ausschließlich nur Einsen als Einträge. Die Einheitsmatrix ist damit ein Sonderfall einer Diagonalmatrix. Eine übliche Abkürzung ist der lichte Buchstabe 𝟙, eine 1 mit doppelt geschriebenem senkrechten Strich. => Ganzen Artikel lesen …
… dasselbe wie eine => transponierte Matrix
Mathematik
Eine Matrix wird gestürzt oder transponiert [1], wenn man ihre Zeilen zu Spalten und ihre Spalten zu Zeilen gemacht hat. Das ist an einem Beispiel näher erklärt unter dem Synonym => transponierte Matrix
Bedarfsmatrix
Aus Rohstoffen werden Zwischenprodukte und aus den Zwischenprodukten Endprodukte gefertigt. Dabei auftretende Mengenbeziehungen werden in einem sogenannten Gozintographen dargestellt. Die dazugehörige Matrix heißt aber nicht Gozintomatrix sondern korrekt Verflechtungs- oder => Bedarfsmatrix
 Grenzmatrix
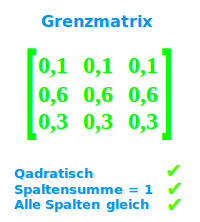
Grenzmatrix
Matrizenrechnung
Wenn A die Übergangsmatrix eines Austauschprozesses ist und wenn es eine Potenz Aⁿ (A^n, meint: A hoch n) gibt, bei der kein Element der Matrix 0 ist und wenn dann alle Spalten (von oben nach unten) der Matrix identisch sind, dann ist die Matrix Aⁿ die Grenzmatrix des Austauschprozesses. => Ganzen Artikel lesen …
Es gibt dazu zwei Methoden
Die Grenzmatrix ist diejenige Matrix, die multipliziert mit einem beliebigen Zustandsvektor direkt zum Vektor der stabilen Verteilung führt. Darüberhinaus ist jede Spalte der Grenzmatrix skalar proportional zum Vektor der stabilen Verteilung. Hier wird die Berechnung kurz vorgestellt. => Ganzen Artikel lesen …
… alle Spalten sind gleich, Definition unter => Grenzmatrix
… von Hand, über lineares Gleichungssystem => Grenzmatrix über LGS
… von Hand, über lineares Gleichungssystem => Grenzmatrix über LGS
Matrizenrechnung
Die Grenzmatrix ist diejenige Matrix, die multipliziert mit einem beliebigen Zustandsvektor direkt zum Vektor der stabilen Verteilung führt. Eine solche Matrix existiert nicht für alle Verteilungen. Wenn sie aber existiert, kann sie über ein lineares Gleichungssystem berechnet werden. Das ist hier kurz skizziert. => Ganzen Artikel lesen …
… von Hand, über lineares Gleichungssystem => Grenzmatrix über LGS
 Grenzmatrix über Taschenrechner
Grenzmatrix über Taschenrechner
Matrizenrechnung
Die Grenzmatrix ist diejenige Matrix, die multipliziert mit einem beliebigen Zustandsvektor direkt zum Vektor der stabilen Verteilung führt. Man kann die Grenzmatrix näherungsweise mit einem Taschenrechner berechnen. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
… von Hand, über lineares Gleichungssystem => Grenzmatrix über LGS
… von Hand, über lineares Gleichungssystem => Grenzmatrix über LGS
… von Hand, über lineares Gleichungssystem => Grenzmatrix über LGS
 Hermitesche Matrix
Hermitesche Matrix
Physik
Eine quadratische Matrix heißt hermitesch wenn sie gleich ihrer adjungiert komplexen Matrix ist. Adjungiert oder auch transponiert und konjugiert nennt man eine Matrix, wenn ihre Spalten zu Zeilen gemacht wurden und gleichzeitig das Vorzeichen des Imaginärteils komplexer Zahlen geändert wurde. Die Benennung erinnert an den französischen Mathematiker Charles Hermite (1822 bis 1901) aus Lothringen. Sie spielen unter anderem in der Quantenphysik eine wichtige Rolle. [3] => Ganzen Artikel lesen …

