2-mal-2-Matrix invertieren
Anleitung
© 2016
- 2025
Basiswissen|
Die Matrix A ist:|
Dann ist ihre Inverse A hoch minus 1:|
Schritt für Schritt|
Probe|
Zahlenbeispiel|
Gibt invertiert|
Probe|
mal|
gibt
Basiswissen
Die Matrix hoch minus eins gerechnet: das Invertieren von Matrizen ist sehr rechenaufwändig. Bei einer kleinen 2-mal-2 Matrix ist dies aber noch gut von Hand möglich. Das Verfahren ist hier kurz erklärt.
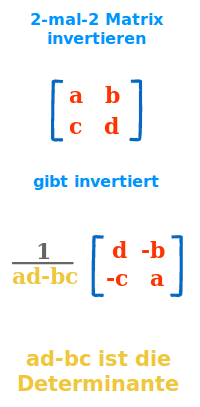
Die Matrix A ist:
a b
c d
Dann ist ihre Inverse A hoch minus 1:
a/[ab-cb]· ...
+d -b
- c +a
Schritt für Schritt
- Rechne ad-bc. Das gibt die Determinante ↗
- Bilde davon den Kehrbruch ↗
- Das ist der Vorfaktor der Inversen
- Vertausche a und d.
- Wechsle das Vorzeichen von c und b.
- Multipliziere a, b, c und d mit dem Vorfaktor.
- Lasse danach den Vorfaktor weg.
- Das Ergebnis ist möglicherweise die inverse Matrix.
Probe
- Das Ergebnis ist nur dann sicher die Inverse, wenn eine Probe aufgeht.
- Multipliziere die inverse Matrix mit der Ausgangsmatrix.
- Wenn dabei eine Einheitsmatrix herauskommt, dann ...
- war das Ergebnis von oben die inverse Matrix.
- Ansonsten gibt es keine inverse Matrix.
Zahlenbeispiel
4 7
2 6
Gibt invertiert
+0,6 -0,7
- 0,2 +0,4
Probe
4 7
2 6
mal
+0,6 -0,7
- 0,2 +0,4
gibt
1 0
0 1
- Das ist eine Einheitsmatrix.
- Also hat man die inverse Matrix bestimmt.