Verfahren
Man geht von dem sogenannten Stammintegral für f(x)=logₖ(x). Ist das kleine k die Eulersche Zahl e, ist die Aufleitung vergleichsweise leicht, in fast allen anderen Fällen eher aufwändig. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
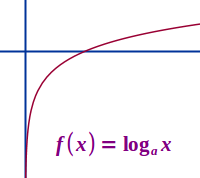Logarithmusfunktion
f(x) = logₖ(x)
In der Analysis: f(x)=ln(x) oder log(x) zu beliebiger Basis: hier sind der Funktionsaufbau und der Zweck kurz beschrieben. => Ganzen Artikel lesen …
F(x) bestimmen
Definition: Als Aufleiten bezeichnet man die Bestimmung einer Stammfunktion F(x) zu einer gegebenen Funktion f(x). Das Aufleiten ist die Gegenoperation des Ableitens: f(x) aufgeleitet gibt F(x). Und F(x) abgeleitet gibt f(x). Hier werden kurz Verfahren dazu vorgestellt. => Ganzen Artikel lesen …
Logarithmusfunktion ableiten
Wie man die erste Ableitung f'(x) bildet
Die Logarithmusfunktion ist nur für positive Funktionsargumente definiert. Der Graph ist überall steigend. Von links nach rechts nimmt die Steigung aber ständig ab, er wird für wachsende x-Werte also flacher. Die Idee zur Bestimmung der Ableitung ist es, einfache Grundformen der Funktion zu verwenden (etwa aus einer Formelsammlung) und dann die Kettenregeln darauf anzuwenden: => Ganzen Artikel lesen …
Beispiele
f(x)=log(x) oder f(x)=ln(x): hier stehen einige Beispiele für Logarithmusfunktionen mit typischen Eigenschaften der Graphen und der Ableitung. => Ganzen Artikel lesen …
f'(x) = cos(x)
Die elementare Cosinusfunktion f(x) = cos(x) abgeleitet gibt f'(x) = -sin(x). Enthält das Argument einen komplexeren Term, benutzt man noch die Kettenregeln: f(x) = cos(4x²-8x) gibt abgeleitet f'(x) = -(8x-8)·sin(4x²-8x). Lies mehr dazu unter => Ableiten über Kettenregel
