Beispiele
lg ⭢ hat als Basis die Zahl 10 (dekadischer Logarithmus), ln ⭢ hat die Basis e (natürlicher Logarithmus), und lb ⭢ hat als Basis die Zahl 2 (binärer Logarithmus). Hier stehen einige Zahlenbeispiele zu Logarithmen mit verschiedenen Basen. => Ganzen Artikel lesen …
Definition
Bei lg 100 ist die 100 der Logarithmand: das, wovon der Logarithmus genommen wird, nennt man Logarithmand oder auch => Numerus
 Logarithmus
Logarithmus
Definition
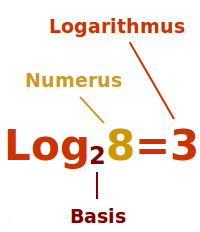
2 hoch was gibt 8? Die Antwort 3 ist auch der Logarithmus. Ein Logarithmus ist eine Hochzahl, die aus einer gegebenen Basis einen gewünschten Potenzwert erzeugt. In der Zeit bevor es Rechenmaschinen gab, erleicherte der Logarithmus den Rechenaufwand erheblich. [1] Das ist hier näher erklärt. => Ganzen Artikel lesen …
 Logarithmieren
Logarithmieren
Definition | Sinn | Anleitung
Das Logarithmieren kann man immer dann nutzen, wenn man eine Gleichung hat, bei der die Unbekannte, oft das x, im Exponenten (Hoch-Term) steht. Bei der Gleichung 4ˣ = 64 steht die Unbekannte, das x im Exponenten. Man kann die Gleichung umformen in log₄64=x. Die linke Seite der Gleichung kann man mit einem Taschenrechner ausrechnen. Man erhält dann x=3. Man hat die Gleichung gelöst über Logarithmieren. => Ganzen Artikel lesen …
… Beispiele unter => Logarithmenbasen
… Rechenregeln unter => Logarithmengesetze
… Rechenregeln unter => Logarithmengesetze
… log von irgendwas mit x, siehe unter => Logarithmusgleichung
… wie lg1000 + lg100 =Siehe unter => Logarithmen mit gleicher Basis addieren
… siehe unter => Logarithmen mit gleicher Basis dividieren
… Übersicht unter => Logarithmusrechnung
… Übersicht unter => Logarithmusrechnung
Rechengesetze
Wie Potenzen haben auch Logarithmen Basen. Sind diese für zwei Logarithmen gleich, kann man Rechnungen oft (aber nicht immer) stark vereinfachen. Da ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Anleitung
lg(100)+lg(10=lg(1000): lg steht für den Logarithmus mit der Basis 10. Bei lg(100) und lg(10) sind die Basen also beide die Zahl 10 und damit gleich. Sind die Basen gleich, werden lediglich die Numeri multipliziert. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
Anleitung
Kein besonderes Gesetz: Logarithmen einzeln ausrechnen, dann teilen. Das ist hier kurz mit Zahlenbeispielen vorgestellt. => Ganzen Artikel lesen …
Anleitung
Es gibt hierzu kein besonderes Gesetz: man muss die Logarithmen einzeln ausrechnen und dann multiplizieren. Das ist hier näher erklärt. => Ganzen Artikel lesen …
Anleitung
Kein besonderes Gesetz: Logarithmen einzeln ausrechnen, dann malnehmen: das ist hier kurz mit Zahlenbeispielen vorgestellt. => Ganzen Artikel lesen …
Anleitung
Kein besonderes Gesetz: Logarithmen einzeln ausrechnen, dann potenzieren: das ist hier kurz mit einem Zahlenbeispiel vorgestellt. => Ganzen Artikel lesen …
Anleitung
lg(1000)-lg(10)=lg(100): lg steht für den Logarithmus mit der Basis 10. Bei lg(1000) und lg(10) sind die Basen also beide die Zahl 10 und damit gleich. Sind die Basen gleich, werden lediglich die Numeri dividiert. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
… siehe unter => Logarithmen mit gleicher Basis multiplizieren
Anleitung
[lg(1000)]³ gibt 9. Und lg(10³) gibt 3: diese zwei unterschiedlichen Fälle, um einen Logarithmus zu potenzieren sind hier mit einem Zahlenbeispiel kurz behandelt. => Ganzen Artikel lesen …
Anleitung
√(lg(10000) gibt 4 und lg(√100) gibt 1: Logarithmen radizieren, also von ihnen die Wurzel zu ziehen, kann zwei verschiedene Dinge bedeuten. Beide Bedeutungen sind hier ausführlich erklärt. => Ganzen Artikel lesen …
… siehe unter => Logarithmengesetze
… wie etwa lg1000-lg100 =Siehe unter => Logarithmen mit gleicher Basis subtrahieren
Beispiele
lg hat als Logarithmus die Basis 10, ld oder auch lb die Basis 2 und ln hat als Basis immer die Eulersche Zahl e. Hier steht eine kurz Übersicht zu diesen Schreibweisen. => Ganzen Artikel lesen …
… Die Zahl, die beim Log-Ausdruck klein unten rechts steht ist die => Basis eines Logarithmus
… Rechenregeln unter => Logarithmengesetze
Rechenregeln
Addieren, subtrahieren, multiplizieren, dividieren und potenzieren und ableiten: hier stehen die wichtigsten Rechenregeln zu Logarithmen in einer kurzen Übersicht. => Ganzen Artikel lesen …
… log von irgendwas mit x, siehe unter => Logarithmusgleichung
… eine Übersicht steht unter => Logarithmusrechnung
Einführung
Logarithmen gibt es zu verschiedenen Basen. Der dekadische Logarithmus ist immer der zur Basis 10. Der natürliche Logarithmus ist immer der zur Basis e. Das waren nur zwei Beispiele. Man kann sich unendlich viele Basen denken. Alle Logarithmen, die zu einer festen Basis gehören bilden ein Logarithmensystem. So würde man alle dekadischen Logarithmen zu eben diesem Logarithmensystem zählen. Hier stehen die wichtigsten Arten im Überblick. => Ganzen Artikel lesen …
… Rechenregeln unter => Logarithmengesetze
… Rechenregeln unter => Logarithmengesetze
… siehe unter => Logarithmengesetze
… siehe unter => Logarithmengesetze

