 LGS
LGS
Übersicht lineare Gleichungssysteme
LGS ist die übliche Abkürzung für ein Lineares Gleichungssystem. Ein LGS besteht aus mehreren linearen Gleichungen für die man eine einzige gemeinsame Lösung sucht. Es gibt verschiedene Arten und Lösungsverfahren, die hier kurz vorgestellt werden. => Ganzen Artikel lesen …
… Magnetische Flussdichte, Abkürzung für => Gauß als Einheit
… [unübliche] Abkürzung für => Kubisches Gleichungssystem
Abkürzung für die Gewichtseinheit Pfund
lbs wird als Gewichtseinheit vor allem in England benutzt. Unter der englischen Bezeichnung pound ist es Teil des angloamerikanischen Maßsystems. Die Buchstaben lbs sind die Mehrzahl von lb. Beide Bezeichnungen werden verwendet. => Ganzen Artikel lesen …
=> Ganzen Artikel lesen …
… [unübliche] Abkürzung für => System lineaer Gleichungen
… oft mit x, y und z, siehe unter => LGS mit drei Gleichungen lösen
… oft mit x, y und z, siehe unter => LGS mit drei Gleichungen lösen
… siehe unter => Altersrätsel lösen
… oft mit x, y und z, siehe unter => LGS mit drei Gleichungen lösen
… oft mit x, y und z, siehe unter => LGS mit drei Gleichungen lösen
… in der Evolutionsbiologie auch => Erfolgslandschaft
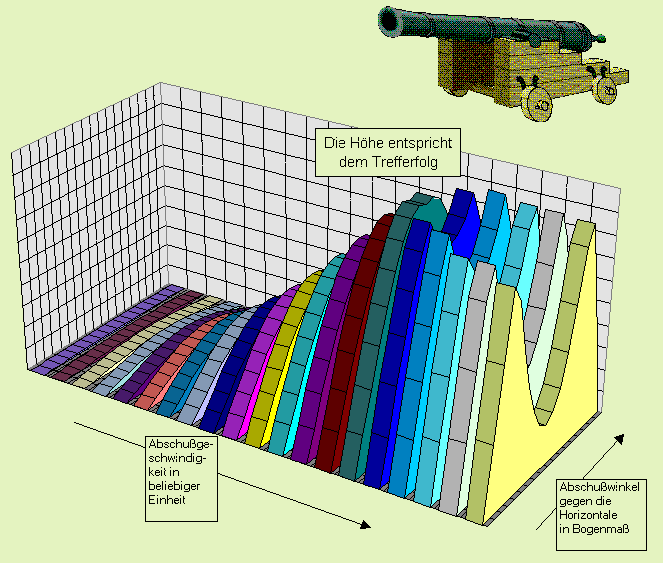 Erfolgslandschaft
Erfolgslandschaft
Evolution
Als Erfolgslandschaft oder auch Erfolgsfläche bezeichnet man die graphische Darstellung der Höhe des Erfolges eines Individuums in Abhängigkeit verschiedener Erfolgsfaktoren. Das Konzept wird vor allem in der Evolutionsbiologie (1) sowie auch der Ökonomik (2) verwendet. In einem dreidimensionalen Koordinatensystem sind die x- und y-Achse die Ausprägung von Erfolgsfaktoren und die Höhe eine Punktes (der z-Wert) die Höhe des Erfolges, die sich bei einer dazugehörigen Ausprägung einstellt. Um lokale Maxima der Erfolgsfläche zu finden, eignet sich zum Beispiel ein => genetischer Algorithmus
Stochastik
Die Worte Erfolgswahrscheinlichkeit [1] und Trefferwahrscheinlichkeit werden in der Stochastik (Wahrscheinlichkeitsrechnung) mit gleicher Bedeutung, also als Synonyme gebraucht. Hier verwenden wir ds Wort => Trefferwahrscheinlichkeit
… siehe unter => LGS lösen [gemischte Aufgaben]
… siehe unter => LGS lösen [gemischte Aufgaben]
… siehe unter => LGS graphisch lösen
… siehe unter => LGS graphisch lösen
Matrizenrechnung
Die Grenzmatrix ist diejenige Matrix, die multipliziert mit einem beliebigen Zustandsvektor direkt zum Vektor der stabilen Verteilung führt. Eine solche Matrix existiert nicht für alle Verteilungen. Wenn sie aber existiert, kann sie über ein lineares Gleichungssystem berechnet werden. Das ist hier kurz skizziert. => Ganzen Artikel lesen …
 Homogenes LGS
Homogenes LGS
Gleichungssystem
Im linearen Gleichungssystem nur Glieder mit Unbekannten. Das ist hier Schritt-für-Schritt definiert. => Ganzen Artikel lesen …
 Inhomogenes LGS
Inhomogenes LGS
Mathematik
Im linearen Gleichungssystem: es gibt Zahlen ohne Unbekannte. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
… oft mit x, y und z, siehe unter => LGS mit drei Gleichungen lösen
… siehe unter => Altersrätsel lösen über x und y
… oft mit x, y und z, siehe unter => LGS mit drei Gleichungen lösen
… oft mit x, y und z, siehe unter => LGS mit drei Gleichungen lösen
… oft mit x, y und z, siehe unter => LGS mit drei Gleichungen lösen
… oft mit x, y und z, siehe unter => LGS mit zwei Gleichungen lösen
… oft mit x, y und z, siehe unter => LGS mit zwei Gleichungen lösen
… oft mit x, y und z, siehe unter => LGS mit drei Gleichungen lösen
… oft mit x, y und z, siehe unter => LGS mit drei Gleichungen lösen
… oft mit x, y und z, siehe unter => LGS mit zwei Gleichungen lösen
Lösungstipps
Bei einem Linearen Gleichungssystem mit drei Gleichungen I, II und III soll man für x, y und z Zahlen finden, die bei jeder der drei Gleichungen als Lösungen klappen. Das geht so: => Ganzen Artikel lesen …
… siehe unter => LGS mit drei Gleichungen
… siehe unter => LGS lösen [gemischte Aufgaben]
… siehe unter => LGS lösen [gemischte Aufgaben]

