Länge
Definition | Beispiele
Als Länge bezeichnet man oft die größte Ausdehnung eines festen Körpers entlang einer geraden Linie. Eine typische Ameise kann zum Beispiel eine Länge von 1 cm haben. => Ganzen Artikel lesen …
Längen
Typische Länge aus dem Alltag
Etwa 10 cm für einen normalen Zeigefinger oder 25 Meter für ein typisches Hallenbad: einige Längen aus dem Alltag sind hier zusammengestellt. => Ganzen Artikel lesen …
Beispiele
Gänse sind sind meist monogam, Männchen und Weibchen sind sehr sehr ähnlich. Sie sind größer als die eng verwandten Enten. Hier stehen einige Beispiele. => Ganzen Artikel lesen …
Hände
Biologie
Menschen, haben eine linke und eine rechte Hand: die linke Hand ist auf der Seite wo auch das Herz ist. Die rechte Hand ist dann entsprechend auf der anderen Seite. Siehe auch => linke Hand
Physik
Als Weg- oder Streckenlänge, oft abgekürzt mit einem kleinem s (Strecke), bezeichnet wie viele Millimeter, Zentimeter, Meter, Kilometer oder auch Lichtjahre lang ein Weg oder eine Strecke ist. Folgt der gedachte Weg dem kürztesten Abstand zwischen zwei Punkten, ist die Weglänge auch gleich der Streckenlänge (immer gerade). Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
… wie lange die Sonne am Himmel steht, auch => lichter Tag
Beispiele
Eine rote Waldameise ist zum Beispiel 1 cm lang. Der Fuß eines Erwachsenen ist etwa 30 cm lang, ein Hallenbad oft 25 m. Und der Fluss Rhein hat eine Länge von 1239 km. Weitere Beispiele stehen unter => Längen
… für große Entfernungen, siehe unter => Astronomische Längenmaße
Liste
Nur eine astronomische Einheit AE bis zur Sonne aber über 8 Lichtjahre bis zum hellen Stern Sirius : für die großen Entfernungen in der Astronomie verwendet man auch entsprechend große Einheiten. Hier stehen einige Beispiele dazu. => Ganzen Artikel lesen …
… kleine alpha in der Physik => thermischer Längenausdehnungskoeffizient
Technischer Fachbegriff [Bergbau]
Siehe auch => Ganzen Artikel lesen …
n in der Stochastik
Ein Bernoulli-Kette ist eine Versuchsreihe aus immer gleich durchgeführten Bernoulli-Experimenten (Treffer oder nicht-Treffer). Beispiel: man würfelt 5 mal und untescheidet nur, ob es eine 6 (Treffer) war oder nicht (nicht-Treffer). Die Länge n der Kette ist hier 5, da man 5 mal gewürfelt hat. Siehe auch => Bernoulli-Kette
Bogenlänge
Mathematik
Die gestreckt gedachte Länge zwischen zwei Punkten entlang einer Linie nennt man die Bogenlänge. Ein Bogen im engeren Sinn ist eine gekrümmte Kurve. Im Zusammenhang mit Längenberechnungen schließt das Wort Bogenlänge aber die Berechnung gerader Teillängen meist mit ein. => Ganzen Artikel lesen …
Formeln
Für Kreisbögen sowie Funktionsgraphen: beides ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Berechnung
Eine Kurve heißt hier: die Linie eines Funktionsgraphen, kurz oft nur Funktionsgraph genannt. Die Bogenlänge ist die Länge dieser Linie zwischen zwei gegebeben Punkten. Die Berechnung ist erklärt unter => Bogenlänge über Integralrechnung
Berechnung
Wie lang ist der Graph einer Funktion f(x) zwischen zwei Punkten A und B? Die Berechnung kann recht kompliziert werden. Sie ist erklärt unter => Bogenlänge über Integralrechnung
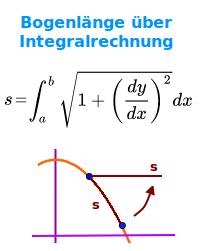Bogenlänge über Integralrechnung
∫√[1+(f'(x))²]·dx
Auf einem Funktionsgraphen (Kurve) sind zwei Punkte gegeben. Die Bogenlänge s zwischen diesen Punkten ist definiert als der Abstand des gerade gestreckt gedachten Bogens. Die Länge kann mit Hilfe eines Integrals berechnet werden. => Ganzen Artikel lesen …
Brechungszahlen nach Wellenlänge
Zahlenwerte
Der Brechungsindex einer Zahl gibt an, wie viel mal so langsam Licht in diesem Material ist, wie im Vakuum. Je größer die Zahl desto langsamer das Licht. Und desto stärker wird es auch an Grenzen zwischen verschiedenen Stoffen gebrochen. Die Brechungszahl hängt aber nicht nur vom Stoff selbst sondern auch (geringfügig) von der Wellenlänge des Lichts ab. Diesen Abhängigkeit nennt man auch Dispersion. Dazu hier einige Beispiele. => Ganzen Artikel lesen …
Elektron-Photon
Beim Stoß an einem (quasi) freien, ruhenden Elektron übernimmt dieses einen Teil der Energie E des Photons, dessen Energie sich auf E' vermindert - es handelt sich um einen elastischen Stoß. Je größer seine Ausgangsenergie, desto vollständiger kann die Energie übertragen werden Bei einem „Streifschuss“ mit Phi=0 behält das Photon fast seine ganze Energie, bei einem „Frontalzusammenstoß“ mit Phi= 180 Grad wird das Photon zurückgestreut und verliert maximal an Energie. Dabei ist Phi der Winkel, um den sich die Bewegungsrichtung des Photons ändert. => Ganzen Artikel lesen …
De-Broglie-Wellenlänge
Quantenphysik
Die Wellenlänge λ ist eine typische Welleneigenschaft, die man in der Quantenphysik aber auch einem Teilchen zuordnet. Eine Masse m, eine Geschwindigkeit v und ein Impuls p hingegen gehören ausschließlich ins Bild der Teilchen. Über die Planck-Konstante h wird dient die Gleichung λ = h/p oder auch λ = h/(mv) als Scharnier zwischen der Teilchen- und der Wellenvorstellung von materiellen Quantenobjekten, etwa Elektronen. => Ganzen Artikel lesen …
Physik
Die de-Broglie-Wellenlänge ist innerhalb der Quantenphysik eine Formel zum Wechsel von der Teilchen in die Wellenvorstellung. Um einem schnellen Teilchen der Ruhemasse m eine Frequenz f zuordnen zu können, rechnet man: => Ganzen Artikel lesen …
… Linie einmal quer durch das Quadrat, Genaueres unter => Quadratdiagonale
Diagonalenlänge
Geometrie
Die Länge einer Linie von einer Ecke zu einer gegenüberliegenden Ecke quer durch eine flache Figur oder einen Körper. Wie man eine solche Längere berechnet steht unter => Diagonalen berechnen
… Linie einmal quer durch das Quadrat, Genaueres unter => Quadratdiagonale
… Linie einmal quer durch das Quadrat, Genaueres unter => Quadratdiagonale
… Linie einmal quer durch das Quadrat, Genaueres unter => Quadratdiagonale
… Linie einmal quer durch das Quadrat, Genaueres unter => Quadratdiagonale
… Linie einmal quer durch das Quadrat, Genaueres unter => Quadratdiagonale
Übersicht
Ungleichseitig, gleichschenklig oder gleichseitig: Dreiecke kann man nach den Längen ihrer Seiten unterscheiden oder nach ihren Winkeln. Hier ist die Unterscheidung nach den Seitenlängen kurz vorgestellt. => Ganzen Artikel lesen …
… die Länge der drei Seiten zusammenaddieren, mehr unter => Dreiecksumfang
… die Länge der drei Seiten zusammenaddieren, mehr unter => Dreiecksumfang
… die Länge der drei Seiten zusammenaddieren, mehr unter => Dreiecksumfang
a+b+c
Zur Berechnung addiert man die Längen der drei einzelnen Seiten. Das Ergebnis ist der => Dreiecksumfang
… die Länge der drei Seiten zusammenaddieren, mehr unter => Dreiecksumfang
… die Länge der drei Seiten zusammenaddieren, mehr unter => Dreiecksumfang
