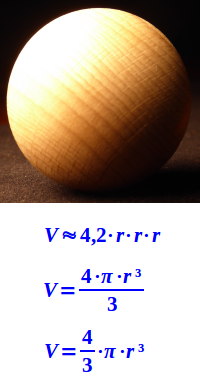Kugelvolumen
Anschaulich
4/3 mal pi mal Radius hoch drei: das Volumen V oder den Rauminhalt einer Kugel kann man zum Beispiel angeben in Litern (l), Kubikzentimetern (cm³) oder Kubikmetern (m³). Zur Berechnung gibt es eine exakte Formel. Es genügt, wenn man den Radius oder den Durchmesser kennt. => Ganzen Artikel lesen …
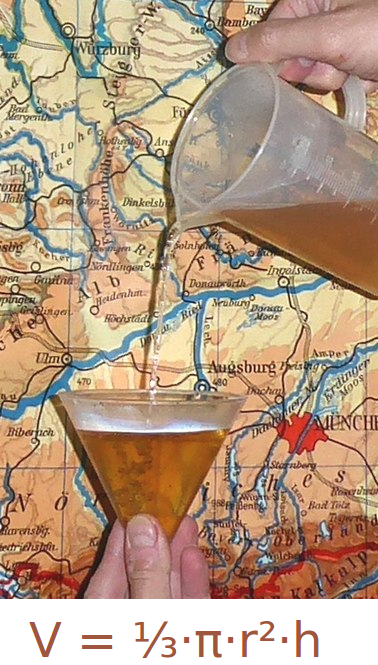Kegelvolumen
V = ⅓·π·r²·h
Ein Kegel ist ein spitzer Körper mit kreisförmiger Grundfläche. Sein Volumen V kann zum Beispiel angegeben werden in Kubikmetern (m³), Kubikzentimern (cm³) oder Litern. Hier werden der Sinn und die Berechnung kurz erklärt. => Ganzen Artikel lesen …
Verweise
- => Planetenvolumina
… ... Rauminhalt eines rettungsringartigen Körpers => Torusvolumen
Rauminhalt (Volumen) eine Hohlkugel
Eine Hohlkugel ist eine Kugel, die aber innen einen wiederum kugeligen Hohlraum hat. Dabei wird angenommen, dass die Hülle überall gleich dick ist. Mit Volumen einer solchen Kugel kann man drei Dinge meinen. => Ganzen Artikel lesen …
Halbkugelvolumen
Geometrie
Es werden drei verschiedene Formeln für das Volumen einer halben Kugel vorgestellt. Es genügt, wenn der Radius r der Halbkugel gegeben ist. Jede der drei Formeln liefert ein korrektes Ergebnis. Man kann sich eine der drei Formeln aussuchen. => Ganzen Artikel lesen …
Praxisversuch
Das Wort Volumen heißt auf deutsch Rauminhalt. Man meint damit wieviel Platz im Raum irgendeine Sache braucht. Als Einheit für kleinere Gegenstände nimmt man oft einen Kubikzentimeter. Wenn ein Würfel einen Zentimeter lang, breit und hoch ist, dann braucht er genau einen Kubikzentimeter Raum. Ein Kubikzentimeter ist genauso viel Raum wie ein Milliliter. Bei festen Sachen redet man meistens von Kubikzentimetern, bei Flüssigkeiten eher von Millilitern. Wir wollen jetzt herausfinden, wie viel Raum eine Kugel mit einem Durchmesser von 5 Zentimetern braucht. => Ganzen Artikel lesen …
Kugelvolumen berechnen
V = 4·π·r³:3
4 mal Pi (etwa 3,14) mal Radius-hoch-3 und alles geteilt durch 3: neben dieser Formel gibt es noch weitere. Diese werden hier kurz vorgestellt und Schritt-für-Schritt erklärt. => Ganzen Artikel lesen …
Herleitung
Wie kommt man aus einfachsten Grundlagen zum Volumen einer Kugel? Eine Lösung bietet die Integralrechnung. => Ganzen Artikel lesen …
… Formel unter => Kugelvolumen
