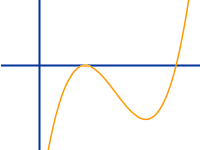
 Kubische Funktion
Kubische Funktion
x³
Jede Funktion, die man umwandeln kann in die Form f(x) = ax³ + bx² + cx + d heißt kubisch. Das x³ muss mindestens einmal vorkommen. Andere Glieder dürfen, müssen aber nicht vorkommen. Eine kubische Funktion ist immer auch eine ganzrationale Funktion. => Ganzen Artikel lesen …
 Funktion
Funktion
f(x)
f(x)=4x+8 ist eine typische mathematische Funktion: man kann für x eine beliebige Zahl einsetzen. Die Rechnung gibt dann einen y-Wert als Ergebnis der eindeutig dem eingesetzten x-Wert zugeordnet ist. Das ist die Grundidee einer Funktion. Der Gedanke wird hier ausführlich erklärt. => Ganzen Artikel lesen …
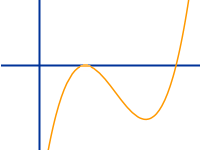 Kubische Funktionen
Kubische Funktionen
Arten und Beispiele
Reinkubisch, gemischtkubisch sowie ohne und mit absolutem Glied: hier stehen einige wichtige Arten kubischer (hoch drei) Funktionen sowie dazu auch konkrete Beispiele mit Zahlenwerten. => Ganzen Artikel lesen …
f(x) = ax³+bx²+cx+d
Kubik heißt bei Funktionen so viel wie „hoch 3“. Eine Kubikfunktion ist eine Funktion mit x³. Das übliche Fachwort dafür ist => kubische Funktion
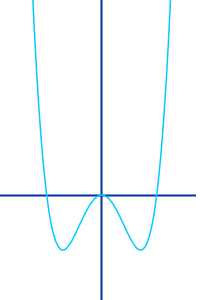 Quartische Funktion
Quartische Funktion
f(x)=T(x⁴)
Ganzrationale Funktion mit höchstens x hoch 4: als quartisch bezeichnet man eine Funktion, die man in die Form f(x) = a·x⁴ + b·x³ + c·x^2 + d·x + e bringen kann. Ein anderer, gleichbedeutender Name ist ganzrationale Funktion vierten Grades. Das Wort quartisch steht für 4 und bezeichnet die höchste vorkommende Potenz der unabhängigen Variablen x. => Ganzen Artikel lesen …
Definition
Jede Funktion - und nur solche Funktionen - die man umformen kann in f(x) = ax³ + d heißen reinkubisch. Der Funktionsterm ist eine Plusminus-Kette bei dem als Summanden nur das x als dritte Potenz (hoch drei) vorkommt und zusätzlich erlaubt, aber nicht gefordert, ist noch eine reine Zahl ohne x. => Ganzen Artikel lesen …
Beispiele
f(x) = x³-8 ist eine reinkubische Funktion: in Anlehnung an reinquadratische Funktionen sind in reinkubischenFunktionen nur Terme mit x³ und absolute Glieder erlaut. Hier stehen einige Beispiele dazu. => Ganzen Artikel lesen …
… f(x)=Siehe unter => Kubische Normalparabel
Definition
Gemischtkubisch nennt man eine ganzrationale Funktion dritten Grades bei der neben dem kubischen Glied mit x³ auch mindestens ein quadratisches Glied mit x² oder ein lineares Glied mit x vorkommt. Beispiele stehen unter => gemischtkubische Funktionen
Beispiele
Gemischtkubisch nennt man eine ganzrationale Funktion dritten Grades bei der neben dem kubischen Glied mit x³ auch mindestens ein quadratisches Glied mit x² oder ein lineares Glied mit x vorkommt. Hier stehen Beispiele dazu. => Ganzen Artikel lesen …
… Graph von Funktion mit x-hoch-3 => Parabel dritten Grades
… z. B. von Siehe unter => Parabel dritter Ordnung
… z. B. von Siehe unter => Parabel dritter Ordnung
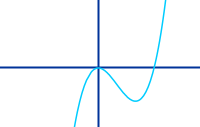 Kubische Funktion ableiten
Kubische Funktion ableiten
Anleitung
f(x) = x³-8x²-5x+2 gibt f'(x) = 3x²-16x-5: eine kubische Funktion wird oft auch ganzrationale Funktion dritten Grades genannt. Die höchste Potenz von x ist die Zahl 3. Bei der Ableitung entsteht immer eine quadratische Funktion. Das Ableiten ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Versuch
An einem Haken befestigt hängt ein Gummiband frei senkrecht nach unten. Am unteren Ende des Gummibandes ist ein S-Haken befestigt. => Ganzen Artikel lesen …
… z. B. von Siehe unter => Parabel dritter Ordnung
Definition
f(x) = 2x³+9 oder auch f(x) = 2x³-1x²+4x+9 sind Beispiele: das absolute Glied ist die Zahl ohne x, also hier die +9 am Ende der Funktionsterme. Das ist hier näher erklärt. => Ganzen Artikel lesen …
Definition
f(x) = 4x³ oder auch f(x) = 4x³-2x²+1x sind Beispiele für kubische Funktionen ohne absolutes Glied: es kommen nur Glieder mit x, x² und x³ vor, aber keine Glieder ganz ohne x. Das ist hier näher erklärt. => Ganzen Artikel lesen …
… siehe unter => y-Achsenabschnitt von kubischen Funktionen
… z. B. x³+4x² = x²(x+4) => Nullstellen von kubischen Funktionen über Faktorisieren
… z. B. von Siehe unter => Parabel dritter Ordnung
… siehe => Nullstellen von kubischen Funktionen bestimmen
… siehe => Nullstellen von kubischen Funktionen bestimmen
… siehe => Nullstellen von kubischen Funktionen bestimmen
… mehrere Methoden unter => Nullstellen von kubischen Funktionen bestimmen
… siehe => Nullstellen von kubischen Funktionen bestimmen
… siehe => Nullstellen von kubischen Funktionen bestimmen
… siehe => Nullstellen von kubischen Funktionen bestimmen
… siehe unter => Satz über rationale Nullstellen
… mehrere Methoden unter => Nullstellen von kubischen Funktionen bestimmen
… ist am ehesten eine => ganzrationale Funktion
… siehe => Nullstellen von kubischen Funktionen bestimmen
… siehe => Nullstellen von kubischen Funktionen bestimmen
… siehe => Nullstellen von kubischen Funktionen bestimmen
… siehe => Nullstellen von kubischen Funktionen bestimmen

