∫: Definition
Das bestimmte Integral ist immer ein einzelner Zahlenwert. Ein unbestimmtes Integral hingegen ist eine Funktion. Neben dieser mathematischen Deutung heißt das Adjektiv integral auch so viel wie der wesentliche Teil von einem größeren Ganzen [1]. Hier wird die mathematische Bedeutung des Wortes Integral erklärt. => Ganzen Artikel lesen …
Arten
Als Integral bezeichnet man oft einen Rechenausdruck, eine Stammfunktion oder einen Zahlenwert. Das wird hier kurz an Beispielen vorgestellt. => Ganzen Artikel lesen …
… gibt 0, mehr unter => 0 aufgeleitet
… gibt x, mehr unter => 1 aufgeleitet
… ist 0,5x², mehr unter => x aufgeleitet
… ist 0,5x², mehr unter => x aufgeleitet
Basisinfos
Das kleine a und das kleine b stehen oft für die linke, untere (a) und die rechte, obrere (b) Grenze eines Integrationsintervalles. Mehr dazu unter => Integrationsgrenzen
… Anleitung unter => Mittelwert von Funktionswerten über Integral
Lösungsidee
Man kann den durchschnittlichen Funktionswert f(x) einer Funktion relativ leicht mit Hilfe der Integrechnung bestimmen. Eine Erkärung dazu steht auf => Mittelwert von Funktionswerten über Integral
 Bestimmtes Integral
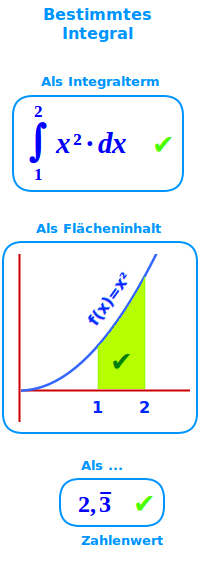
Bestimmtes Integral
Definition
Ein Integralterm mit angegebene Grenzen, auch der entsprechende Zahlenwert: das Wort Integral ist nicht sehr präzise. Es wird sowohl für eine Stammfunktion F(x) benutzt wie auch für Integralterme mit und ohne Angaben von Grenzen. Ein bestimmtes Integral hingegen ist immer ein Integralterm mit zwei als Zahlen angegebenen Grenzen. Ein solcher Term kann immer als Zahl ausgerechnet werden. Diese Zahl heißt oft auch bestimmtes Integral oder besser: Integralwert => Ganzen Artikel lesen …
F(b) - F(a)
Das bestimmte Integral von f(x)=6x soll berechnet werden in den Grenzen von 2 bis 4. Zuerst Stammfunktion bilden: F(x)=6x²/2 oder kurz: F(x)=3x². Dann rechnen: F(4)-F(2) = 48-12 = 36. Die Zahl 36 ist das Rechenergebnis für das bestimmte Integral. Der Rechenweg wird unten Schritt-für-Schritt erläutert. => Ganzen Artikel lesen …
 Bogenlänge über Integralrechnung
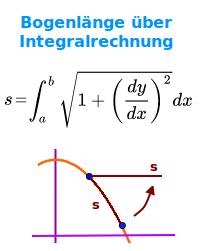
Bogenlänge über Integralrechnung
∫√[1+(f'(x))²]·dx
Auf einem Funktionsgraphen (Kurve) sind zwei Punkte gegeben. Die Bogenlänge s zwischen diesen Punkten ist definiert als der Abstand des gerade gestreckt gedachten Bogens. Die Länge kann mit Hilfe eines Integrals berechnet werden. => Ganzen Artikel lesen …
… Zahl + oder - am Ende einer Aufleitung => Integrationskonstante
Integrationskonstante
Jede Funktion F(x), die abgeleitet wieder f(x) heißt Stammfunktion. Da konstante Zahlen beim Ableiten zu 0 werden (verschwinden), kann es unendlich viele Stammfunktion für ein f(x) geben. Das wird berücksichtigt über die sogenannte => Integrationskonstante
Integrationskonstante
Das große C steht in der Integralrechnung oft für eine konstante Zahl: f(x)=2x gibt aufgeleitet F(x) = x²+C. Das C ist die => Integrationskonstante
… gibt sin(Siehe unter => cosinus x aufgeleitet
Analysis
Die Differentialrechnung baut auf der Idee der Ableitung auf, also der Steigung eines Graphen an einem Punkt. Kerngedanke der Integralrechnung ist die Aufleitung, veranschaulicht als Flächeninhalt von Kurven. Beide Gebiete werden zusammengefasst zur => Analysis
… das Integtral von einem => Integral
… das Zeichen dafür ist ein => ∭
Lehrsatz
Der durchschnittliche Funktionswert einer Funktion f(x) kann leicht über ein Integrall bestimmt werden. Mehr dazu unter => Mittelwert von Funktionswerten über Integral
… ist e hoch x, mehr unter => e hoch x aufgeleitet
Analysis
Ein eigentliches Integral ist der Zahlenwert, der zu einer rundum vollständig begrenzten Fläche gehört, die von einem Funktionsgraphen, senkrechten Linien an den Intervallgrenzen und einer der beiden Koordinatenachsen gebildet wird. Das Gegenstück dazu ist das => uneigentliches Integral
… gibt x, mehr unter => 1 aufgeleitet
Begriffsklärung
Es gibt eigentlich nur einen Hauptsatz. Er ist aber oft unterteilt in zwei einzelne Aussagen. Mehr dazu unter => Hauptsatz der Differential- und Integralrechnung
… über Integrieren, siehe unter => Fläche unter der Kurve berechnen
… über Integrieren, siehe unter => Fläche unter der Kurve berechnen
A = ?
Gesucht ist die Fläche zwischen einem Funktionsgraphen und der x-Achse. Das eine zentrale Fragestellung der Integralrechnung. Es wird erklärt auf der Seite => Fläche unter der Kurve berechnen
A = ?
Über integrieren kann man viele Flächen recht einfach berechnen. Die dazu nötigen Methoden stehen unter => Fläche unter der Kurve berechnen
A = ?
Flächen meint hier: zwischen Funktionsgraphen und der x-Achse. Wie das praktisch ausgeführt werden kann steht unter => Fläche unter der Kurve berechnen
… über Integrieren, siehe unter => Fläche unter der Kurve berechnen
… über Integrieren, siehe unter => Fläche unter der Kurve berechnen
Analysis (Funktionsgraphen)
Mit Hilfe der Integralrechnung kann man unter anderem Flächeninhalte berechnen, bei denen einer oder mehrere Funktionsgraphen Ränder bilden. Es werden verschiedene Grundtypen entsprechender Aufgaben vorgestellt. => Ganzen Artikel lesen …
… über Integrieren, siehe unter => Fläche unter der Kurve berechnen
A = ?
Die Integralrechnung bietet verschiedene Methoden, um unregelmäßige und Flächen mit geschwungenen Rändern zu berechnen. Mehr dazu unter => Fläche unter der Kurve berechnen
… über Integrieren, siehe unter => Fläche unter der Kurve berechnen

