Hypotenuse
Definition
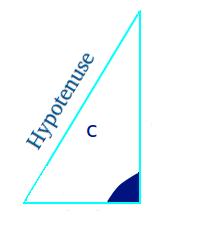
Eine Hypotenuse gibt es nur in einem rechtwinkligen Dreieck. Die Hypotenuse ist immer die längste der drei Seiten. Sie liegt immer gegenüber vom rechten Winkel. Das ist hier näher erklärt. => Ganzen Artikel lesen …
Hypothese
Wissenschaft
Als Hypothese bezeichnet meine eine durch Beobachtung oder logisches Denken überprüfbare Aussage, oft abgeleitet aus einer bereits bestehenden und glauwürdigen Theorie. [3] Newtons Gesetze (z. B. F=m·a) gelten im gesamten Universum. Diese Behauptung wird von vielen Wissenschaftlern als Grundlage für aufwändige Berechnungen benutzt. Sie passt gut auf die Bewegung der Planeten um die Sonne. Es gibt aber Zweifel. => Ganzen Artikel lesen …
Rhetorik
Als Hypotypose bezeichnet man in der Rhetorik die Vergegnwärtigunge eines Sachverhaltes als anschauliche, sprachliche Gestaltung [1]. So kann der abstrakte Gedanke, dass alle Einwohner Griechenlands (Hellas) sich bereit zeigten, gemeinsam in einen Krieg zu ziehen anschaulich auch als Hypotypose ausgedrückt werden: 'da sprangen auf ihre Füße Hellas' Männer all' [2]. Ähnlich einer Hypotypose ist die => Allegorie
Beispiele
==== Hypothesentest ==== => Ganzen Artikel lesen …
… Erklärung mit Zeichenanleitung => Höhe über der Hypotenuse
… kurze Stichworte zum Weiterlesen unter => Hypotenuse berechnen
… kurze Stichworte zum Weiterlesen unter => Hypotenuse berechnen
Höhe über der Hypotenuse
Definition
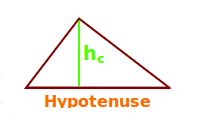
Die Höhe über der Hypotenuse ist die kürzeste Strecke von der Hypotenuse zur Spitze mit dem rechten Winkel. => Ganzen Artikel lesen …
Höhe über der Hypotenuse berechnen
Verfahren
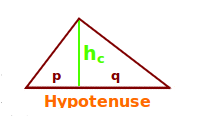
Die Höhe über der Hypotenuse ist eine Strecke, die im rechten Winkel eines Dreiecks beginnt. Sie geht von dort auf kürzestem Weg zur Hypotenuse (längste Strecke im Dreieck). Sie trifft immer mit 90° auf die Hypotenuse. => Ganzen Artikel lesen …
.png "Hypotenuse heißt wörtlich aus dem Altgriechischen übersetzt: die Herunterhängende. Das wird in dem Bild verdeutlicht.")
Hypotenuse
Etymologie
Das altgriechische Wort Hypotenuse lässt sich wörtlich als die herabhängende Seite übersetzen. Woher diese Bezeichnung stammt ist unklar. Möglicherweise würden Dreiecke zu Lehrzwecken so aufgehängt, dass diese Seite nach unten zeigt. Siehe auch => Hypotenuse
Hypotenuse berechnen
Anleitung
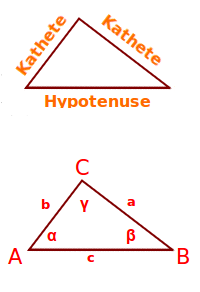
Jedes rechtwinklige Dreieck - und auch nur rechtwinklige Dreiecke - haben eine Hypotenuse. Die Hypotenuse ist immer die längste Seite im Dreieck. Kennt man die Länge der beiden kürzeren Seiten, also der Katheten, dann kann man daraus über Pythatoras direkt die Länge der Hypotenuse berechnen. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
… Anleitung unter => Hypotenuse über Sinus
… kurze Stichworte zum Weiterlesen unter => Hypotenuse berechnen
… Anleitung unter => Hypotenuse über Sinus
… Anleitung unter => Hypotenuse über Sinus
Berechnung
Wie man die Hypotenuse mit dem Cosinus ausrechnet: die Rechnung gilt für alle rechtwinkligen Dreiecke. Der Rechenweg ist hier ausführlich Schritt-für-Schritt erklärt. => Ganzen Artikel lesen …
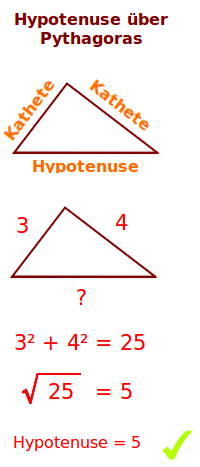Hypotenuse über Pythagoras
Man kennt die Länge der zwei kürzeren Seiten
Man hat ein rechwinkliges Dreieck gegeben. Bekannt sind die längen der beiden kürzeren Seiten, also der Katheten. Daraus kann man immer die Länge der längsten Seite, der Hypotenuse berechnen. Das wird hier ausführlich erklärt. => Ganzen Artikel lesen …
Berechnung
Die Hypotenus ist immer die längste Seite in einem rechtwinkligen Dreieck. Man kann sie auf verschiedene Weisen berechnen, zum Beispiel auch mit dem Sinus. Das ist hier ausführlich Schritt-für-Schritt erklärt. => Ganzen Artikel lesen …
… einer von zwei der möglichen => Hypotenusenabschnitte
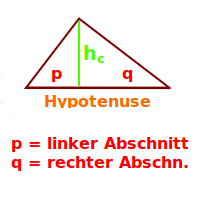Hypotenusenabschnitte
p und q
Die Hypothenuse c ist die längsten Seite in einem rechtwinkligen Dreieck. Die Höhe über der Hypotenuse teilt der Fußpunkt der Höhe die Hypotenuse in die zwei Abschnitt p und q. Das wird hier näher erklärt. => Ganzen Artikel lesen …
c = ?
Die Hypotuse ist die längste Seite in einem rechtwinkligen Dreieck. Ihre Länge kann man berechnen über Pythagoras, sinus, cosinus oder noch weitere Methoden. Mehr dazu unter => Hypotenuse berechnen
… Rechenweg auf => Hypotenuse über Pythagoras
… Anleitung unter => Hypotenuse über Sinus
… Anleitung unter => Hypotenuse über Sinus
… kurze Stichworte zum Weiterlesen unter => Hypotenuse berechnen
… Rechenweg auf => Hypotenuse über Pythagoras
… Anleitung unter => Hypotenuse über Sinus
… Anleitung unter => Hypotenuse über Sinus
… Anleitung unter => Hypotenuse über Sinus
… Schema wie es geht unter => Hypotenuse über Pythagoras
… Rechenweg auf => Hypotenuse über Pythagoras
Wie man eine unbekannte Hypotenusenlänge ausrechnet
Wenn man von einem rechtwinkligen Dreieck die Länge der beiden Katheten kennt, dann kann man die Länge der Hypotenuse immer so ausrechnen: => Ganzen Artikel lesen …
… Anleitung unter => Hypotenuse über Sinus
