 Gerade zeichnen aus Steigung und Punkt
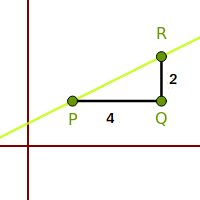
Gerade zeichnen aus Steigung und Punkt
Schritt-für-Schritt für m=0,5 und P(2|2)
Es wird Schritt für Schritt erklärt, wie man aus einem gegebenen Punkt und einer gegebenen Steigung eine Gerade in einem xy-Koordinatensystem zeichnet. => Ganzen Artikel lesen …
 Gerade
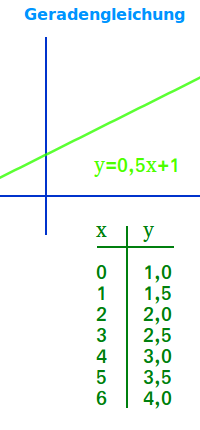
Gerade
Übersicht
Eine Gerade in der Mathematik ist eine Linie ohne Ecken, Lücken, Kurven oder Enden: sie ist unendlich lang gedacht. Die kürzeste Verbindung zwischen zwei Punkten liegt immer auf einer Geraden. Hier werden Geraden in verschiedenen Teilgebieten der Mathematik kurz vorgestellt. => Ganzen Artikel lesen …
 Steigung
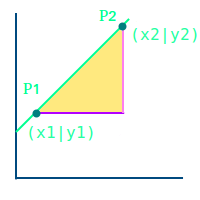
Steigung
Übersicht
Steigung sagt, wie steil etwas nach oben oder unten geht. Man kann eine Steigung als Zahl angeben, zum Beispiel: etwas hat eine Steigung von 2,5. Das meint: Eine Strecke geht zweieinhalb mal so weit senkrecht nach oben wie waagrecht nach vorne. Es werden verschiedene Gebiete aus der Mathematik vorgestellt. => Ganzen Artikel lesen …
Logisches UND
x=3 UND x=4 heißt: x soll gleichzeitig 3 und 4 sein. Das ist ein logischer Widerspruch. Besser ist oft das logische ODER: Möchte man beispielweise als zwei Lösungen einer pq-Formel angeben, dass einmal x=3 und einmal x=4 als Lösung gilt, dann schreibt man: x=3 ODER x=4; kurz: x=3 v x=4. Lies mehr unter => Logisches UND
Mathematik
Dezimalpunkt, Tausendertrennpunkt und Multiplikations-Punkt: diese drei wichtigen Bedeutungen sind hier kurz erklärt. Viele weitere Bedeutungen stehen unter => Punkte
 Geradengleichung aus Steigung und Punkt
Geradengleichung aus Steigung und Punkt
Anleitung
Von einer Geraden kennt man einen Punkt, z. B. (5|20). Man kennt auch die Steigung, z. B. m= 1,5. Gesucht ist die Gleichung in der Form y=mx+b oder auch y=mx+n. Das Verfahren ist hier Schritt für Schritt erklärt. => Ganzen Artikel lesen …
… Verfahren und Aufgaben unter => Geradengleichung aus Steigung und Punkt
… Verfahren und Aufgaben unter => Geradengleichung aus Steigung und Punkt

