Basiswissen

1. Schritt

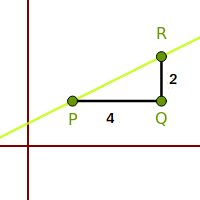
• Man trägt den gegebenen Punkt P ein:
  

• Nimm den gegebenen Punkt, zum Beispiel wäre er (2|2).
  

• Die erste Zahl ist der x-Wert des Punktes.
  

• Die zwei Zahl ist der y-Wert des Punktes.
  

• Nimm die erste Zahl und gehe an diese Stelle auf der x-Achse.
  

• (Die x-Achse ist die waagrechte Achse von links nach rechts.)
  

• Bleibe gedanklich mit dem Finger auf dieser Stelle.
  

• Jetzt gehst du von dort aus so weit senkrecht nach oben, wie die zweite Zahl sagt.
  

• Hier müssen wir also zwei nach oben gehen.
  

• Beschrifte den Punkt dort mit P.
  

2. Schritt

• Jetzt geht man von P aus irgendeine waagrechte Strecke nach rechts.
  

• Man wählt oft glatte Zahlen dafür. Gut wäre hier zum Beispiel die 4.
  

• Tipp: Man nimmt am besten eine Zahl, die man gleich leicht mit m malnehmen kann.
  

• Wir gehen im Beispiel hire also 4 Schritte nach rechts und beschriften den Punkt mit Q.
  

• Zur Kontrolle: der Punkt Q liegt bei (6|2).
  

• Jetzt nimmt man den Zahlenwert der Steigung m, hier also 0,5.
  

• Man rechnet dann die waagrecht gegangene Strecke mal der Steigung.
  

• Wenn man also 4 Kästchen nach rechts gegangen ist, kämen jetzt 2 Kästchen heraus.
  

• Jetzt geht man von Q aus so viele Kästchen nach oben (falls m eine positive Zahl ist).
  

• Wenn die Steigung negativ wäre, dann würde man so viele Kästchen nach unten gehen.
  

• Wir gehen also jetzt von Q aus drei Kästchen nach oben.
  

• Dort markiert man wieder einen Punkt. Wir nennen ihn hier R.
  

• R hätte im Beispiel die Koordinaten (6|4).
  

3. Schritt:

• Gerade fertigstellen
  

• Verbinde jetzt die zwei Punkte P und R mit einem Lineal.
  

• (Der Punkt Q ist jetzt nicht mehr wichtig.)
  

• Verlängere diese Strecke sinnvoll.
  

• Das ist jetzt die fertige Gerade