Geometrie
Man kann eine Gerade sowohl rein geometrisch als auch algebraisch als einen geometrischen Ort angeben: einmal a) als die Menge aller Punkte, die zu jedem von zwei gegebenen festen Punkten denselben Abstand haben und b) als visualierte Lösungsmenge einer linearen Gleichung wie etwa y+2x=10. Beide Möglichkeiten sind hier kurz vorgestellt. => Ganzen Artikel lesen …
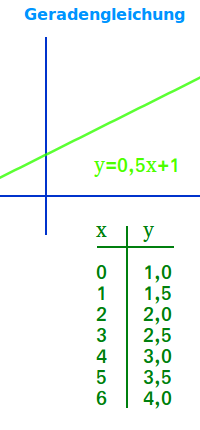Gerade
Übersicht
Eine Gerade in der Mathematik ist eine Linie ohne Ecken, Lücken, Kurven oder Enden: sie ist unendlich lang gedacht. Die kürzeste Verbindung zwischen zwei Punkten liegt immer auf einer Geraden. Hier werden Geraden in verschiedenen Teilgebieten der Mathematik kurz vorgestellt. => Ganzen Artikel lesen …
Wo
Als Ort bezeichnet man heute einen festen Punkt „in einem Raum, einem Gelände oder auf der Erdoberfläche“ [1]. In der Physik gibt man einen Ort meist an über Koordinaten [2]. Die ursprüngliche Bedeutung beinhaltet noch die Idee von etwas Letztem [3], was sich in der Bergmannsprache in Begriffen wie wie Ortsbrust oder vor Ort erhalten hat [4]. In der Geometrie ist der Ort eine Menge von Punkten, die eine Gleichung löst [5]. Zur heutigen Bedeutung, insbesondere im Sinn der Physik, siehe den Artikel zu => Ort (Physik)
Definition
Die Parabel ist der geometrische Ort für alle Punkte, die von einem festen Punkt, dem Brennpunkt (Fokus), und von einer festen Geraden, der Leitlinie (Direktrix) gleich weit entfernt sind [1]. Das wird hier näher erklärt. => Ganzen Artikel lesen …
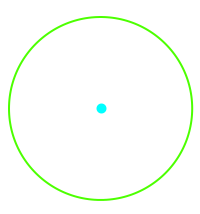
Alle Punkte einer Ebene mit demselben Abstand zu einem festen Mittelpunkt.
Alle Punkte einer Ebene mit demselben Abstand zu einem festen Mittelpunkt bilden zusammen eine Kreislinie, oft kurz auch Kreis genannt. Das ist hier näher erklärt. => Ganzen Artikel lesen …
Geometrischer Ort
Definition
Ein geometrischer Ort ist eine Punktemenge. Die Punkte können dabei alle nach derselben mathematischen Regel oder nach einer sprachlich formulierten Bedingungen erstellt werden. Das ist hier erklärt. => Ganzen Artikel lesen …
