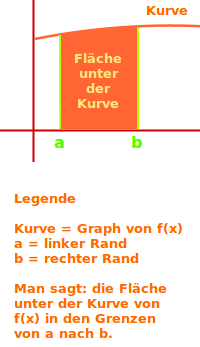
Fläche unter der Kurve berechnen
Anleitungen
Die Fläche unter der Kurve meint immer eine Flächen, die von einem Funktionsgraphen, der x-Achse und eventuell noch von zwei senkrechten Strecken umrandet wird. Es gibt erschiedene Aufgabentypen, die hier kurz vorgestellt sind. => Ganzen Artikel lesen …
Fläche
Mathematik
Eine Fläche ist alltagssprachlich zunächst eine größere Ausdehnung ohne nennenswerte Erhebungen oder Vertiefungen. Man spricht von Eis- und Wasserflächen, von Wandflächen oder Tischflächen. Hier wird kurz erklärt, was Fläche mathematisch bedeutet und was der Unterschied zur Ebene ist. => Ganzen Artikel lesen …
Unter
Naturwissenschaften
Tiefer als etwas anderes: hält man die Hand über den Kopf, dann ist der Kopf unter der Hand: unter der Erde haben Pflanzen oft Wurzeln. Hier einige weitere Beispiele. => Ganzen Artikel lesen …
Bedeutungen
In der Geometrie ist eine Kurve eine zusammenhängende Linie. Sie kann gerade oder auch gebogen sein. Für Funktionen ist Kurve ein Synonym für den Graphen. Beide Bedeutungen werden hier kurz vorgestellt. => Ganzen Artikel lesen …
Berechnen
Definition
Bis auf einen Zahlenwert genau bestimmen. Man kann zum Beispiel den Gesamtpreis von 4 Äpfeln berechnen, wenn man weiß, dass jeder einzelne Apfel 50 Cent kostet. Man rechnet: 4 mal 50 Cent und hat als Gesamtpreis dann 200 Cent oder genau 2 €. => Ganzen Artikel lesen …
… über Integrieren, siehe unter => Fläche unter der Kurve berechnen
… über Integrieren, siehe unter => Fläche unter der Kurve berechnen
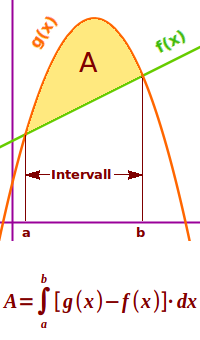Fläche zwischen Kurven berechnen
Integralrechnung
A = F(x)-G(x) über die Differenzenmethode: man hat zwei Graphen in einem Koordinatensystem gegeben. Gesucht ist die Fläche, die zwischen diesen zwei Graphen und zwei weiteren senkrechten Linien, den Integrationsgrenzen a und b liegt. Dazu ist hier eine Berechnungsmethode vorgestellt. => Ganzen Artikel lesen …
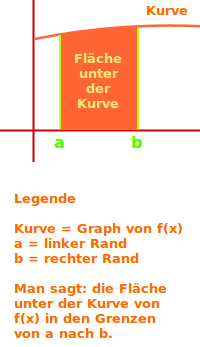Fläche unter der Kurve
Integralrechnung
Die Fläche unter der Kurve ist die Flächen zwischen einer Kurve einer Funktion f(x), der x-Achse und - meistens - einer senkrechten Linie als linker Rand und einer senkrechten Linie als rechter Rand. Diese Definition wird hier Schritt-für-Schritt erklärt. => Ganzen Artikel lesen …
