ℜ
Physik Chemie Grundschule Mathematik I Mathematik II Wissen
Kurze Worte Worte nach Alter Terme Rechner
Mathfeed Physfeed Philfeed
Das Lexikon Die Mission Die Autoren Copyright Impressum
Physik Nachhhilfe 5-10 Physik Nachhilfe 11-13 Chemie Nachhilfe 5-13 Mathe Nachhilfe 5-8 Mathe Nachhilfe 9-10 Mathe Nachhilfe 10-13
☰
1: Faktorisieren

Mathematik

8x+4 kann faktorisiert werden zu 4·(2x+1): faktorisieren heißt so viel wie Ausklammern und dadurch umwandeln in eine Malkette. Die Malkette besteht dann aus einzelnen Faktoren. Daher kommt das Wort. Das ist hier ausführlich erklärt. => Ganzen Artikel lesen …
2: Faktorisiere

… klammere aus, wandle um in eine Malkette, mehr unter => faktorisieren
3: autorisieren

ist richtig geschrieben. Eine häufige Falschschreibung ist: authorisieren
4: Faktorisierung

Mathematik

Man kann Zahlen und Terme auch als Plus- oder Malketten schreiben. Das Umwandeln einer Zahl in eine Malkette nennt man Faktorisieren. Ein Faktor ist alles, was malgenommen wird. Das ist hier kurz erklärt. Lies mehr zu Durchführung unter => faktorisieren
5: Bruch faktorisieren

Umwandlung

Man hat einen Bruch wie zum Beispiel 3/4. Faktorisieren heißt, man soll ihn als Produkt mit Faktoren schreiben, also als Malkette. Eine Möglichkeit ist 3/1 mal 1/4. Allgemein gilt: a/b = a/1 mal 1/b. Damit ist der Bruch faktorisiert. Siehe auch => faktorisieren
6: Eine Ganzrationale Gleichung dritten Grades lösen über Faktorisieren

… siehe unter => Kubische Gleichungen über Faktorisieren
7: Faktorisieren für plus

… z. B. 14=8+3+1, siehe unter => zerlegen

Siehe auch
8: Faktorisieren in Pluskette

… Zahl in Pluskette umformen => Zahlpartition
9: Faktorisieren in Summe

… z. B. 9 = 4+3+2

Faktorisieren heißt: in eine Malkette zerlegen: 20 faktorisiert ist z. B. 4·5 oder 2·10. Man kann jede Zahl und jeden Term auch als Pluskette schreiben: 20x kann man zum Beispiel als 18x+2x schreiben. Die Pluskette als Ganzes ist dann eine Summe oder ein Summenterm. Die einzelne Teile heißen Summanden oder auch Glieder. Mehr unter => zerlegen
10: Faktorisieren mit plus

… Zahl in Pluskette umformen => Zahlpartition
11: Faktorisieren Nullstellen

… aus Funktionsterm Malkette machen => Nullstellen über Faktorisieren
12: Faktorisieren nur für plus

… Zahl in Pluskette umformen => Zahlpartition
13: Funktionsnullenstellen über Faktorisieren

… aus Funktionsterm Malkette machen => Nullstellen über Faktorisieren
14: Funktionsnullstellen über Faktorisieren

… aus Funktionsterm Malkette machen => Nullstellen über Faktorisieren
15: Ganzrationale Gleichung dritten Grades über Faktorisieren

… siehe unter => Kubische Gleichungen über Faktorisieren
16: Ganzrationale Gleichung vom Grad drei über Faktorisieren

… siehe unter => Kubische Gleichungen über Faktorisieren
17: Ganzrationale Gleichungen dritten Grades lösen über Faktorisieren

… siehe unter => Kubische Gleichungen über Faktorisieren
18: Ganzrationale Gleichungen dritten Grades über Faktorisieren

… siehe unter => Kubische Gleichungen über Faktorisieren
19: Ganzrationale Gleichungen dritten Grades über Faktorisieren lösen

… siehe unter => Kubische Gleichungen über Faktorisieren
20: Gleichungen lösen über Faktorisieren

Beispiele

0 = x²-4x kann man umformen in 0 = x·(x-4). Durch die Umformung ist auf der rechten Seite ein Produkt, das heißt eine Malkette entstanden. Eine solche Umwandlung nennt man eine Faktorisierung. Die einzelnen Teile der Malkette nennt man Faktoren. Aus diesen Faktoren kann man die Lösungen der Gleichung oft direkt ablesen. Das ist hier Schritt-für-Schritt erklärt. => Ganzen Artikel lesen …
21: Gleichungen über Faktorisieren

Verweise

- => Quadratische Gleichungen über Faktorisieren
22: Kubisch über Faktorisieren

… siehe unter => Kubische Gleichungen über Faktorisieren
23: Kubische Funktionen faktorisieren

… z. B. x³+4x² = x²(x+4) => Nullstellen von kubischen Funktionen über Faktorisieren
24: Kubische Gleichungen faktorisieren

… als Lösungsmethode, steht unter => Kubische Gleichungen über Faktorisieren
25: Kubische Gleichungen über Faktorisieren

Lösungsverfahren

0 = 4x³-2x² gibt faktorisiert (ausgeklammert) die Gleichung 0 = 2x²·(2x-1). In dieser Form kann man die Nullstellen über den Satz vom Nullprodukt leicht bestimmen: man betrachtet sich die Teile der Malkette einzeln: 2x² wird 0, wenn man für x die 0 einsetzt und 2x-1 wird 0, wenn man für x die Zahl ½ einsetzt. Die Lösungen der Gleichung sind also 0 und ½. Das ist hier ausführlich erklärt. => Ganzen Artikel lesen …
26: Nullstelle einer Parabel über Faktorisieren

… siehe unter => Nullstellen von quadratischen Funktionen über Faktorisieren
27: Nullstelle einer Parabelgleichung über Faktorisieren

… siehe unter => Nullstellen von quadratischen Funktionen über Faktorisieren
28: Nullstellen berechnen über Faktorisieren

… aus Funktionsterm Malkette machen => Nullstellen über Faktorisieren
29: Nullstellen bestimmen über Faktorisieren

… aus Funktionsterm Malkette machen => Nullstellen über Faktorisieren
30: Nullstellen faktorisieren

… aus Funktionsterm Malkette machen => Nullstellen über Faktorisieren
31: Nullstellen finden über Faktorisieren

… aus Funktionsterm Malkette machen => Nullstellen über Faktorisieren
32: Nullstellen über Faktorisieren

Verfahren

Faktorisieren heißt einen Term in eine Malkette, auch Produkt genannt, umzuformen. Aus Malketten kann man Nullstellen von Funktionen oft direkt ohne weiteres Rechnen ablesen. Dazu sind hier einige häufige Verfahren vorgestellt. => Ganzen Artikel lesen …
33: Nullstellen von Funktion über Faktorisieren

… aus Funktionsterm Malkette machen => Nullstellen über Faktorisieren
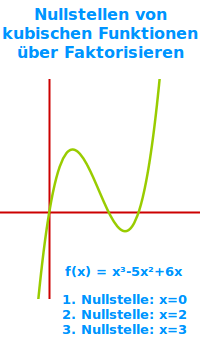34: Nullstellen von kubischen Funktionen über Faktorisieren

Übersicht

f(x) = x³-x² kann man faktorisieren und erhält dann f(x) = x²·(x¹-1). Für diese umgeformte Variante kann man drei Nullstellen direkt ablesen: 0, -1 und 1. Das Lösungsverfahren ist hier erklärt. => Ganzen Artikel lesen …
35: Nullstellen von kubischen Funktionen über Faktorisieren

… siehe => Nullstellen von kubischen Funktionen bestimmen
Zur Startseite von Rhetos
Startseite
Impressum
© 2010-2023


Startseite Impressum Feedback © 2010-2023