 Exponentialfunktion
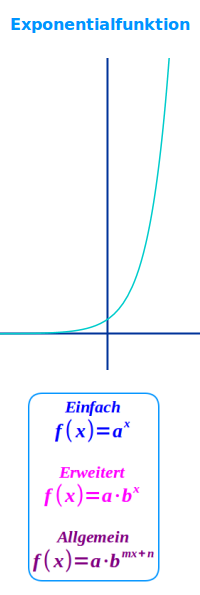
Exponentialfunktion
Funktion mit x im Exponenten
Jede Funktion, die sich umformen lässten in f(x) = a·b^T(x) heißt Exponentialfunktion. Das T(x) ist irgendein Term, bei dem eines oder mehrere x'se vorkommen. Bei einer Exponentialfunktion kommt immer ein x in einem Exponenten vor, daher auch der Name. Ist die Basis b der Potenz die Eulersche Zahl e, spricht man auch von einer e-Funktion. Das ist hier näher erklärt. => Ganzen Artikel lesen …
 Exponentialfunktionen
Exponentialfunktionen
Arten
Von f(x) = a^x bis zu f(x) = 400-e^(-x): hier stehen verschiedene Arten von Exponentialfunktionen mit Fachworten benannt und kurz erklärt. => Ganzen Artikel lesen …
… Graph einer hoch-x-Funktion => Exponentialkurve
Mathematik
r·e^(i·phi) nennt man die Exponentialform einer komplexen Zahl. f(x)=4ˣ ist eine Exponentfunktion. In dem Term 2³ ist die 3 der sogenannte Exponent: hier sind verschiedene Formen mit der Bezeichnung exponential oder exponentiell kurz vorgestellt. => Ganzen Artikel lesen …
… Graph einer hoch-x-Funktion => Exponentialkurve
… a^x abgeleitet gibt a^x·ln(a), allgemeiner unter => Exponentialfunktion ableiten
 Allgemeine Exponentialfunktion
Allgemeine Exponentialfunktion
Definition
f(x) = a·b^(mx+n) - das ist eine Exponentialfunktion weil die Variable, hier das x, im Exponenten einer Potenz steht. Die Basis der Potenz, hier das b, ist dabei irgendeine feste reelle Zahl. Dazu ist hier kurz erläutert. => Ganzen Artikel lesen …
… umformen, siehe unter => Exponentialfunktion in e-Funktion
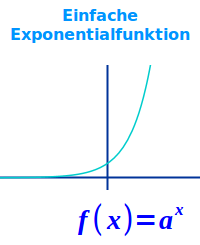 Einfache Exponentialfunktion
Einfache Exponentialfunktion
f(x) = a^x
Bei der einfachen Exponentialfunktion gibt es nur eine Basis hoch der Variablen (meist x). Zu diesem Term wird nichts hinzuaddiert oder er wird auch nicht mit irgendwas malgenommen. Wird der Term über weitere Rechenarten erweitert, entsteht die sogennante => erweiterte Exponentialfunktion
… a^x abgeleitet gibt a^x·ln(a) => Ableitungsregeln
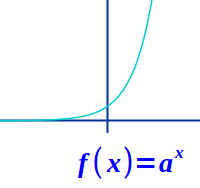 Einfache Exponentialfunktion ableiten
Einfache Exponentialfunktion ableiten
f(x) = a^x abgeleitet gibt f'(x) = ln(a)·a^x
Die einfache Exponentialfunktion besteht aus einer Konstanten als Basis einer Potenz und dem x als Exponent dieser Potenz. Es dürfen keine weiteren Zahlen oder Rechnungen damit verbunden sein. => Ganzen Artikel lesen …
Erklärung am Beispiel der Punkte (2|9) (5|243)
Hat man zwei Punkte gegeben, dann kann es sein, dass es gar keine Exponentialfunktion gibt, die durch beide Punkte geht. Um herauszufinden, ob es doch geht und wie dann die Funktionsgleichung aussieht, kannst du immer so vorgehen: => Ganzen Artikel lesen …
… f(x) = a^x, siehe unter => einfache Exponentialfunktion
 Erweiterte Exponentialfunktion
Erweiterte Exponentialfunktion
Anschaulich
f(x) = a·b^x oder auch c·a^x oder ähnlich: die erweiterte Exponentialfunktion passt gut als Modell für viele Prozesse aus der Wirklichkeit, etwa zu Zinseszinsen oder zur Radioaktivität. Die einzelnen Bestandteile der Funktion haben oft eine anschauliche Bedeutung. Diese sind hier kurz vorgestellt. => Ganzen Artikel lesen …
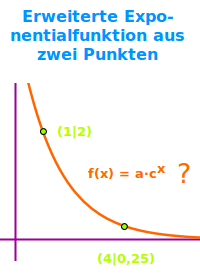 Erweiterte Exponentialfunktion aus zwei Punkten
Erweiterte Exponentialfunktion aus zwei Punkten
f(x)=a·bˣ
Man hat zwei oder mehr Punkte eines Graphen von einer Exponentialfunktion. Mit diesen Angaben kann man eine Funktionsgleichung erstellen. Gesucht sind die Koeffizienten a und b. Für sie sollen am Ende konkrete Zahlenwerte eingesetzt werden. Das Verfahren verläuft analog zum aufstellen einer Geradengleichung oder einer Parabelgleichung aus zwei Punkten: man setzt beide Punkte in die Grundform (Bauplan) der Funktionsgleichung ein. Dadurch ensteht ein lineares Gleichungssystem (LGS), das man dann löst. Die Ergebnisse des LGS sind die gesuchten Koeffizienten des Funktionstermes. Das Dach ^ steht für hoch. b^x meint dasselbe wie b-hoch-x. => Ganzen Artikel lesen …
Beispiele
Die erweiterte Exponentialfunktion hat die Form f(x) = a·b^x. Gegenüber der einfachen Exponentialfunktion f(x) = b^x ist sie um den Faktor a erweitert. Dieser Faktor steht für den Anfangswert entsprechend dem x-Wert 0. Setzt man für x die Null in die Funktionsgleichung ein, erhält man: f(0) = a. für diesen Funktionstypen stehen hier Beispiele. => Ganzen Artikel lesen …
 Exponentialfunktion ableiten
Exponentialfunktion ableiten
Anleitung
Am leichtestens ist f(x)=eˣ, nicht viel schwerer ist f(x)=aˣ. Neben diesen einfachen Formen der e-Funktionen wird hier auch erklärt, wie man kompliziertere Varianten von Exponentialfunktionen ableitet, zum Beispiel f(x)=e⁽⁴ˣ⁻²⁾ oder f(x)=4⁽⁴ˣ⁻²⁾. Die Grundidee ist immer die sogenannte Kettenregel. => Ganzen Artikel lesen …
Zwei Fälle
f(x) = a^x ist die allgemeine und f(x) 0 e^x die spezielle e-Funktion. Für beide ist hier kurz die Aufleitung, das heißt eine Stammfunktion, angegeben. => Ganzen Artikel lesen …
Bestimmen
f(x) = a·b^x - kann auch geschrieben werden als y = a·b^x: eine solche (Funktions)gleichung kann aus Punktangaben, Texten oder sonstigen Informationen aufgestellt werden. Mehr dazu unter => Exponentialgleichung aufstellen
Analysis
Man hat den Graphen einer Exponentialfunktion. Gesucht ist die Funktionsgleichung in der Form f(x) = a·b^x. Die Grundidee ist, dass man zwei beliebige Punkte aus dem Graphen abliest. Damit kann man dann immer eindeutig eine Funktionsgleichung erstellen. Das Verfahren ist erklärt unter => Exponentialfunktion aus zwei Punkten
… siehe unter => Exponentialfunktion aus zwei Punkten
… zum Wasserabkühlkurve, siehe unter => Exponentialgleichung aus Versuch
 Exponentialfunktion aus zwei Punkten
Exponentialfunktion aus zwei Punkten
Lösungsmethoden
Man hat zwei Punkte gegeben, etwa aus einem Funktionsgraphen. Gesucht ist eine Funktionsgleichung als Exponentialfunktion. Exponentialfunktionen gibt es in verschiedenen Varianten. Jede Variante hat einen eigenen Lösungsweg. Diese sind hier kurz vorgestellt. => Ganzen Artikel lesen …
… siehe unter => Exponentialfunktion aufstellen
Umformen
Aus f(x) = a·bˣ wird f(x) = a·eˣˡⁿ⁽ᵇ⁾: die Ausgangsfunktion ist eine Exponentialfunktion, die zweite Funktion ist sowohl eine Exponential- als auch eine e-Funktion. Die e-Funktion ist ein Sonderfall einer allgemeinen Exponentialfunktion. Die Umformung und die Herleitung sind hier kurz vorgestellt. => Ganzen Artikel lesen …
… Anleitung unter => Exponentialfunktion in e-Funktion
… ist erklärt unter => Exponentialgleichung nach Änderungsfaktor umstellen
… ist erklärt unter => Exponentialgleichung nach Exponent umstellen
… siehe unter => Exponentialgleichung nach Startwert umstellen
f(x)=0
Eine Exponentialfunktion kann - muss aber nicht - eine Nullstelle haben. Die Berechnung kann recht kompliziert werden. Mehr dazu unter => Nullstellen von Exponentialfunktionen bestimmen
… siehe unter => Nullstellen von Exponentialfunktionen bestimmen
… Graph einer hoch-x-Funktion => Exponentialkurve
… wie e^Siehe unter => Funktionen mit Parametern
… siehe unter => Nullstellen von Exponentialfunktionen bestimmen
Liste
Das Stichwort Funktion steht eher für funktionale Abhängigkeiten. Man will dann wissen, was y macht, wenn sich x verändert. Das ist bei den hier gesammelten Textaufgaben nicht der Fall. Man will hier meistens nur einen einzigen Zahlenwert bestimmen. Das fällt in das Themengebiet (Bestimmungs)Gleichungen. Dort sind dann die klassischen Textaufgaben zu Exponentialgleichungen: Baktieren, Zinsen, Weltbevölkerung, Kondensatorladungen etc. Siehe unter => Exponentialfunktionen Textaufgaben

