Dreisatz
Rechenart
Wenn an zwei Zweigen 10 Blätter sind, wie viele Blätter wären dann an drei solchen Zweigen? Solche - und ähnliche - Aufgabentypen werden hier betrachtet unter dem Überbegriff => Dreisatzrechnung
Zweisatz
Erklärung | Beispiele
Ein Käfer hat 6 Beine. Wie viele Beine haben dann vier Käfer zusammen? Das ist eine typische Zweisatzaufgabe. => Ganzen Artikel lesen …
Brisanz
Sprengung
Als Brisanz bezeichnet man in der Sprengtechnik das Zertrümmerungsvermögen eines Explosivstoffes. Der Brisanzwert nach Kast ist das Produkt aus Ladedichte, spezifischer Energie und Detonationsgeschwindigkeit (bei Sprengstoffen) oder Abbrandgeschwindigkeit (bei Pyrotechnischen Sätzen). Hier stehen einige Beispiele. => Ganzen Artikel lesen …
Eine Liste sinnvoll zusammengehörender Daten
Datensatz ist ein Begriff der oft in der Informatik verwendet wird. In der Statistik spricht man oft von Datenreihen (etwas ähnliches). Datensätze werden oft als Tabellen oder Listen dargestellt. => Ganzen Artikel lesen …
… => Umgekehrt proportionaler Dreisatz
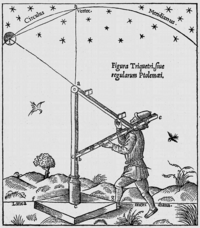
Dreistab
Astronomie
Der Dreistab war ein großes hölzernes Gerät zur Messung astronomischer Winkel. Das Gerät wurde schon in der Antike, zum Beispiel von Claudius Ptolemäus genutzt (100 bis 160 n. Chr.) aber auch später noch von Nikolaus Kopernikus (1473 bis 1543). Der große praktische Vorteil war, dass man den zu messenden Winkel bequem zeitlich versetzt zum eigentlichen Vorgang des Anvisierens auf einer Skala ablesen konnte [1]. Kopernikus soll die meisten seiner Messungen mit einem Dreistab gemacht haben [1, Seite 175]. Gemessen wird der sogenannte => Zenitwinkel
… meint dasselbe wie => Umgekehrt proportionaler Dreisatz
Doppelter Dreisatz
Lösungsbeispiel
4 Maurer machen in 3 Tagen 5 Meter Mauer. Wie lange bräuchten dann 6 Maurer für 20 Meter? Diesen Aufgabentyp bezeichnet man als doppelten Dreisatz oder auch Kettensatz. Die Lösungsidee hier sieht zunächst langwierig und umständlich aus, da sie ausführlich erklärt wird. Hat man die Rechnung aber einmal verstanden, ist der Lösungsweg sehr kurz unnd einfach. Man kann damit jeden doppelten Dreisatz auf eine immer gleiche Weise lösen. => Ganzen Artikel lesen …
… veraltet für => umgekehrt proportionaler Dreisatz
… doppelt so viel x gibt auch doppelt so viel y, siehe unter => proportionaler Dreisatz
… doppelt so viel x, halb so viel y, siehe unter => umgekehrt proportionaler Dreisatz
… => Umgekehrt proportionaler Dreisatz
Lösungsschema für proportionale Dreisatzaufgaben
f(x) = 0,8·x passt als Funktionsgleichung auf: „Man bezahlt 4 € für 5 Bananen. Wie teuer sind dann 7 Banane? Antwort über: f(7) = 0,8·7. Antwort: 7 Bananen kosten 5 € und 60 ct. Hier wird beschrieben, wie man darauf kommt. => Ganzen Artikel lesen …
Lösungsschema für proportionale Dreisatzaufgaben
Beim proportionalen Dreisatz funktioniert der Spruch: wenn das eine doppelt so viel wird, wird auch das andere doppelt so viel. Immer wenn das geht, kann man den Dreisatz über eine Verhältnisgleichung lösen. Diese Lösungsmethode kannst du verwenden, wenn du einfache Verhältnisgleichungen schon lösen kannst. Wenn du das noch nicht kannst, dann suche dir ein anderes Verfahren (es gibt mehrere). => Ganzen Artikel lesen …
… => Umgekehrt proportionaler Dreisatz
Methode
Dreisatz ist ein Überbegriff für verschiedene Aufgaben- bzw. Lösungsverfahren. Es werden Tipps zum Erkennen mit Hilfe der Hauptwort-Methode gegeben. => Ganzen Artikel lesen …
Dreisatzaufgaben
Sammlung
Man unterscheidet den proportionalen (normalen), den den umgekehrt proportionalen und den doppelten Dreisatz. Daneben gibt auch einen sogenannten Zweisatz. Hier sind Aufgaben dazu zusammengestellt. Die eigentlichen Aufgaben stehen unter qck (Quickcheck). => Ganzen Artikel lesen …
Dreisatzrechnung
Grundbegriffe
Die Dreisatzrechnung, auch Schlussrechnung genannt, fasst Dreisätze und ähnliche Aufgabentypen zusammen. Eine typische Frage ist: wenn an zwei Zweigen 10 Blätter sind, wie viele Blätter wären dann an drei solchen Zweigen? Hier folgt eine Gesamtübersicht zu diesem Thema. => Ganzen Artikel lesen …
Dreisatzversuche
Anleitungen
Wenn 10 Holzwürfel zusammen 7,2 Gramm wiegen, wie schwer sind dann 36 dieser Würfel? solche und ähnliche Aufgaben zum praktischen Nachstellen als Freihandversuch sind hier zusammengestellt. => Ganzen Artikel lesen …
… siehe unter => Umgekehrt proportionale Gleichung aufstellen
… siehe unter => Umgekehrt proportionale Gleichung aufstellen
Gerader Dreisatz
… x verdoppelt sich, y auch => proportionaler Dreisatz
Proportional
Wenn drei Eier 180 Gramm wiegen, wie schwer wären dann 2 Eier? Antwort: 120 Gramm. Diese Art von Dreisatz heißt => proportionaler Dreisatz
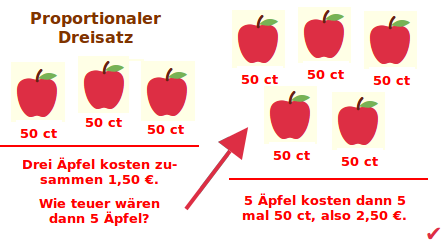
Proportionaler Dreisatz
Definition
Der „normale“ oder „einfache“ Dreisatz, zum Beispiel: 3 Äpfel kosten 1,50 Euro. Wie teuer wären 5 Äpfel? Antwort: 5 Äpfel würden dann 2,50 Euro kosten. Das ist der normale oder proportionale Dreisatz. => Ganzen Artikel lesen …
… => Umgekehrt proportionaler Dreisatz
… => Umgekehrt proportionaler Dreisatz
… => Umgekehrt proportionaler Dreisatz
Doppelt so viel vom Einen gibt halb so viel vom anderen
Ein gutes Beispiel für diese Art von Dreisatz ist der Zusammenhang von Geschwindigkeit und Reisezeit. Wenn ich doppelt so viel „Geschwindigkeit habe“, dann gibt das nur „halb so viel“ Reisezeit. => Ganzen Artikel lesen …
… => Umgekehrt proportionaler Dreisatz
Ungerader Dreisatz
… x verdoppelt sich, y halbiert sich => umgekehrt proportionaler Dreisatz
