 Dreieck
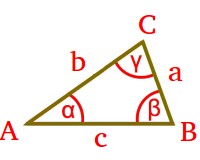
Dreieck
ABC
Definition: Jede flache (2D) Figur mit genau drei Ecken und genau drei geraden Verbindungslinien zwischen den Linien ist ein Dreieck. Ein Dreieck ist damit eine Sonderfall eines Vielecks. Eine Themenübersicht steht auf der Seite => Dreiecksrechnung
 Dreiecke
Dreiecke
⯅ ⯆ ⯇ Systematik und Beispiele
Dreiecke sind flache (2D) Figuren mit genau drei Ecken und nur geraden Verbindungslinien zwischen den Ecken. Dreiecke teilt man nach ihren Seitenlängen und nach ihren Innenwinkel ein. Auf dieser Seite folgt eine Übersicht verschiedener Dreiecksarten. Eine Übersicht zum ganzen Thema steht auf => Dreieck
… 0; 3; 6; 9; 12; 15 und so weiter: alle Zahlen aus der => Dreierreihe
 Kreiseck
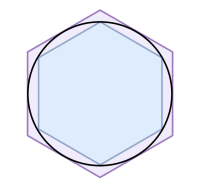
Kreiseck
… Siehe unter => Polygonkreis
Ein Vieleck mit immer mehr Ecken kann immer feiner einer Kreis nachbilden. Mehr dazu unter => Polygonkreis
 Geodreieck
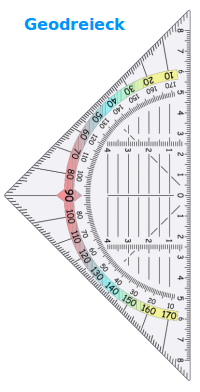
Geodreieck
📐 Gleichschenkliges, rechtwinkliges Dreieck als Zeichenhilfe
Die längste Seite heißt Linealkante, Nulllinie oder Hypotenuse. Die beiden kurzen Seiten heißen Schenkel oder auch Katheten. Die Mitte der längsten Seite heißt Nullmarke. Die Linie von der Nullmarke zu gegenüberliegenden Spitze heißt Mittellinie. => Ganzen Artikel lesen …
Arten
Ein Dreieck ist per Definition immer flach und 3D steht für dreidimensional, also räumlich. Obwohl sich die Definition eines Dreiecks und Räumlichkeit zunächst auszuschließen scheinen, kann 3D-Dreieck sinnvolle Bedeutungen haben. Diese sind hier kurz vorgestellt. => Ganzen Artikel lesen …
… das mit den Ecken A, B und C, mehr dazu unter => Standarddreieck
… gibt immer 180 Grad, mehr unter => Innenwinkelsumme für Dreiecke
… gibt immer 180 Grad, mehr unter => Innenwinkelsumme für Dreiecke
… gibt immer 180 Grad, mehr unter => Innenwinkelsumme für Dreiecke
 3D-Dreiecke
3D-Dreiecke
Verschiedene Varianten: Dreieckpyramide, Tetraeder, Dreieckprisma, Dreieck im Raum
Das Wort 3D-Dreieck gibt es in der offiziellen Mathematik nicht. Dreiecke sind per Definition immer flache (also 2D) Gebilde, niemals Körper (also nie 3D). Umgangssprachlich wird es aber öfters benutzt und kann dann veschiedene Dinge meinen. => Ganzen Artikel lesen …
… das mit den Ecken A, B und C, mehr dazu unter => Standarddreieck
Berechnung, Sinn der Grenzwertbildung
Die Ableitung dient dazu, die Steigung eines Graphen an einer bestimmten Stelle, das heißt an einem bestimmten Punkt zu berechnen. Ein Steigungsdreieck hingegen benötigt immer zwei Punkte. => Ganzen Artikel lesen …
… Definition und Beispiele unter => ähnliche Dreiecke
… Definition und Beispiele unter => ähnliche Dreiecke
… Definition und Beispiele unter => ähnliche Dreiecke
 Ähnliche Dreiecke
Ähnliche Dreiecke
Übersicht
Zwei Dreiecke sind ähnlich, wenn sie dieselben Innenwinkel haben. Ihre Form ist damit immer gleich, aber sie dürfen unterschiedlich groß sein. Hier stehen Definitinen und Beispiele. => Ganzen Artikel lesen …
 Ähnliche Dreiecke berechnen
Ähnliche Dreiecke berechnen
Anleitung
Zwei Dreiecke heißen ähnlich, wenn sie dieselben Innenwinkel haben. Damit haben sie auch immer dieselbe Form, sie dürfen aber auch unterschiedlich groß sein. Hier stehen Hinweise für Berechnungen. => Ganzen Artikel lesen …
… mehrere Methoden unter => Ähnliche Dreiecke erkennen
… Anleitung zur Überprüfung unter => ähnliche Dreiecke über Parallelität
… Anleitung zur Überprüfung unter => ähnliche Dreiecke über Parallelität
… Anleitung zur Überprüfung unter => ähnliche Dreiecke über Seitenverhältnisse
Übersicht
Zwei Dreiecke sind ähnlich, wenn sie dieselbe Form und dieselben Innenwinkel haben. Sie dürfen aber zueinander verdreht, verschoben oder auch in der Größe unterschiedlich sein. Wie erkennt man dann zwei zueinander ähnliche Dreiecke? Dazu stehen hier einige Methoden. => Ganzen Artikel lesen …
… Anleitung zur Überprüfung unter => ähnliche Dreiecke über Parallelität
… Anleitung zur Überprüfung unter => ähnliche Dreiecke über Parallelität
… Anleitung zur Überprüfung unter => ähnliche Dreiecke über Seitenverhältnisse
… mehrere Methoden unter => Ähnliche Dreiecke erkennen
… Tipps zur Erkennung unter => ähnliche Dreiecke über Matroschka-Methode
… mehrere Methoden unter => Ähnliche Dreiecke erkennen
 Ähnliche Dreiecke über Augenmaß
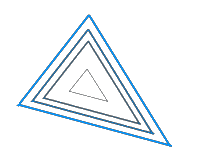
Ähnliche Dreiecke über Augenmaß
… Tipps zur Erkennung unter => ähnliche Dreiecke über Matroschka-Methode
Erkennen
Die kleinen Dreiecke innen, die größeren nach außen: wenn dann die Seiten in einer Richtung immer parallel zueinande sind, dann sind die Dreiecke ähnlich zueinander. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
… zur Erkennung siehe unter => ähnliche Dreiecke über Matroschka-Methode
… Anleitung zur Überprüfung unter => ähnliche Dreiecke über Parallelität
… Anleitung zur Überprüfung unter => ähnliche Dreiecke über Parallelität
… Anleitung zur Überprüfung unter => ähnliche Dreiecke über Seitenverhältnisse

