Differential
Definition
Als Differential bezeichnet man eine hypothetisch unendlich kleine Änderung eines Zahlenwertes. Die übliche Abkürzung ist ein ein lateinisches d oder ein griechisches Delta. Differentiale gelten als mathematisch veraltet und werden in der Mathematik meist ersetzt durch Grenzwerte. Vor allem in praktischen Anwendungsgebieten spielen Differentiale aber eine große Rolle. Eine Übersicht steht unter => Differentiale
Differentiale
d, ∂ oder δ
Differentiale wie etwa dx, δx oder auch δy, beschreiben eine beliebig kleine Änderung eines Wertes. Die Idee des Differentiales bildete historisch die Grundlage der Differential- und Integralrechnung. Es werden verschiedene Arten in verschiedenen Kontexten unterschieden. Diese werden hier kurz vorgestellt. => Ganzen Artikel lesen …
… kleiner x- oder y-Abschnitt, siehe unter => Differential
x-Differential
Definition
Als x-Differential, üblicherweise abgekürzt als dx, bezeichnet man eine theoretisch unendlich kleine Veränderung eines x-Wertes. Das dx ist dabei ein Platzhalter für eine nicht benennbare, unendlich kleine Zahl. Die Idee des Differentials gilt heute mathematisch als veraltet, wird aber vor allem in praktischen Anwendungsgebieten häufig verwendet. Lies mehr dazu unter => Differential
x-Differential
… Beliebig kleine Strecke auf der y-Achse, mehr unter => Differential
dx:dy
Sowohl dx als auch dy nennt man hier ein Differential. Differentiale sind beliebig klein gedachte Unterschiede von Werten, etwa von x- oder y-Werten. In dem Term dy/dx sind sowhl der Zähler als auch der Nenner ein Differential. Der gesamte Term ergibt als Grenzwert die erste Ableitung f'(x). => Ganzen Artikel lesen …
Analysis
Die Differentialrechnung baut auf der Idee der Ableitung auf, also der Steigung eines Graphen an einem Punkt. Kerngedanke der Integralrechnung ist die Aufleitung, veranschaulicht als Flächeninhalt von Kurven. Beide Gebiete werden zusammengefasst zur => Analysis
Definition
Als Differential im Sinne der Mathematik bezeichnet den linearen Anteil des Zuwachses einer Variablen einer Funktion. Formal schreibt man: dy = f'(x)·dx. Siehe auch => Differential
Definition
Eine Differentialgleichung ist eine Gleichung in der eine Ableitung einer gesuchten Funktion [1] und die Funktion selbst enthalten ist [2]. Die Lösung einer Differentialgleichung ist keine Zahl, sondern eine gesuchte Funktion [3] oder Menge von Funktionen [4]. => Ganzen Artikel lesen …
Definition
In einer „Differentialgleichung erster Ordnung ist die gesuchte Funktion y(t) ihrer ersten Ableitung ẏ(t) proportional“ [1]. Die allgemeine Form ist ẏ=C·y(t). Die allgemeine Lösung ist die Exponentialfunktion y(t) = yo·e^(C·t). Dabei sind yo und C beides je eine Konstante. Man überzeuge sich selbst, dass die erste Ableitung ẏ(t) sich nur um ein konstantes Vielfaches von y(t) unterscheidet. Siehe auch => Differentialgleichung zweiter Ordnung
Definition
In einer „Differentialgleichung zweiter Ordnung ist die gesuchte Funktion y(t) proportional zu ihrer zweiten Ableitung ÿ(t)“ [1]. Die allgemeine Form ist ÿ(t)=-C·y(t). Die allgemeine Lösung führt zu trigonometrischen Funktionen wie zum Beispiel y(t)=y₀·sin(√C·t) oder y(t)=y₀·cos(√C·t). Dabei sind y₀ und C jeweils beide konstante Werte. Man überzeuge sich selbst, dass die zweite Ableitung ÿ(t) sich nur um ein konstantes Vielfaches von y(t) unterscheidet [2]. Siehe auch => Differentialgleichung zweiter Ordnung
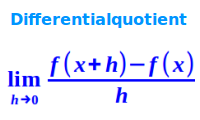Differentialquotient
dy/dx
Der Begriff spielt eine Rolle bei der Bestimmung der Tangententsteigung beziehungsweise der ersten Ableitung einer Funktion. Er wird hergeleitet aus einem Steigungsdreieck. => Ganzen Artikel lesen …
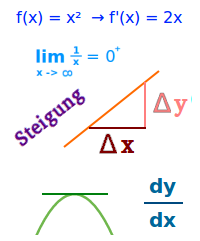Differentialrechnung
Einordnung
f'(x), Steigungen, Hoch- und Tiefpunkte: die Differentialrechnung ist ein Teilgebiet der Analysis. Die Grundidee des gesamten Themas ist die Steigung in einem Punkt. => Ganzen Artikel lesen …
… siehe unter => 13 Formelsammlung Differentialrechnung
… wie x³ zu 6, mehr unter => dritte Ableitung bilden
… wie x² zu Siehe unter => erste Ableitung bilden
Begriffsklärung
Es gibt eigentlich nur einen Hauptsatz. Er ist aber oft unterteilt in zwei einzelne Aussagen. Mehr dazu unter => Hauptsatz der Differential- und Integralrechnung
… siehe unter => Formelsammlung Differentialrechnung
Liste?
Ableitungen, Steigungen, h-Methode, Änderungsraten und so weiter. Eine Liste mit häufig genutzten Formeln steht unter => Formelsammlung Differentialrechnung
… alles rund um f'(x) => Formelsammlung Analysis
F(x) = …
Der Satz besteht aus zwei Teilaussagen. Diese sind erklärt unter => Hauptsatz der Differential- und Integralrechnung
Hauptsatz der Differential- und Integralrechnung
Analysi
F'(x) = f(x) und F(x) = F(b)-F(a): der Hauptsatz besteht aus zwei Teilen. Der erster Teil ist: F'(x)=f(x). Der zweite Teil ist: Integral = F(b)-F(a). Das ist hier näher erklärt. => Ganzen Artikel lesen …
Das dx in ∫f(x)·dx
∫f(x)·dx liest man als: Das Integral von f(x). Das dx ist dabei das sogenannte Differential. Anschaulich steht es für die Breite einer Säule, die man im Rahmen der Säulenmethode zur Berechnung der Fläche zwischen Graph und x-Achse verwendet. Die Bedeutung des Integrationsdifferentials ist anschaulich erklärt im Artikel zum => Integralzeichen
∂f
Eine Funktion mit mehreren unabhängigen Variablen kann oft als 3D-Fläche im Raum veranschaulicht werden. An einen beliebigen Punkt einer solchen Fläche kann oft eindeutig eine Tangentialebene angelegt werden. Das partielle Differential ∂f ist dann die Änderung des Funktionswertes auf dieser Tangentialebene, wenn man den x oder y Werte um ∂x oder ∂y ändert. => Ganzen Artikel lesen …
Term für die größte Steigung
Das totale Differential ist ein Term. Er gibt für höherdimensionale Funktionen an, in welche Richtung und wie steil von einem Punkt aus das Gefälle ist. Lies mehr unter => totale Ableitung
… wie x² zu 2, mehr unter => zweite Ableitung bilden
