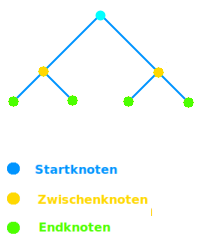
Baumdiagramm
… für Wahrscheinlichkeiten => Baumdiagramm (Stochastik)
… jeder Strich mit einem Knoten am Anfang, siehe auch => Baumdiagramm
… a meint Beschleunigung, siehe unter => Beschleunigung-Zeit-Diagramm
… a steht für Beschleunigung, siehe unter => Beschleunigung-Zeit-Diagramm
… jeder Strich mit einem Knoten am Anfang, siehe auch => Baumdiagramm
Definition und Übersicht
Diagramm nennt man eine graphische Darstellung von Daten und Zahlen. => Ganzen Artikel lesen …
.png "Ein klassisches Baumdiagramm für einen zweistufigen Zufallsversuch")
Baumdiagramm (Stochastik)
Aufbau
Ein Baumdiagramm, auch Ereignisbaum [2] genannt, wird oft von oben nach unten oder links nach rechts gezeichnet. In der Wahrscheinlichkeitsrechnung steht es oft in Verbindung mit der Pfad- und Summenregel. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
… siehe unter => Baumdiagramm aus Vierfeldertafel
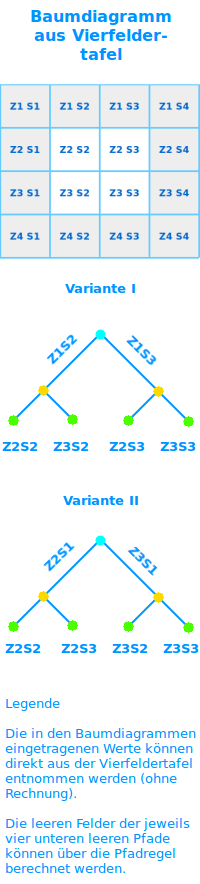Baumdiagramm aus Vierfeldertafel
Stochastik
Aus einer Vierfeldertafel kann man immer auch ein Baumdiagramm erstellen (und umgekehrt). HIer stehen zwei Methoden zur Umwandlung dazu. => Ganzen Artikel lesen …
… für Stochastik => Wahrscheinlichkeitsbaum zeichnen
… siehe unter => Baumdiagramm aus Vierfeldertafel
Stochastik
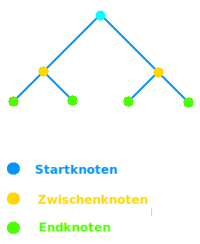
Den Startpunkt eines Baumdiagramms bezeichnet man als Wurzel [1] oder auch Start- oder Anfangsknoten. Die Wurzel ist der Punkt, an dem das Baumdiagramm anfängt sich zu verzweigen. Anders als bei echten Bäumen ist die Wurzel bei senkrecht gezeichneten Baumdiagrammen oben, der Baum steht also auf dem Kopf. Bei waagrecht liegenden Baumdiagrammen ist die Wurzel links gezeichnet. Siehe mehr unter => Startknoten
.png "Am Ende des Versuches hat man ein Baumdiagramm: die bedingten Wahrscheinlichkeiten stehen dann an den unteren Ästen der zweiten Stufe, zwischen den gelben und den grünen Knoten.")
Bayes-Schüssel-Versuch (Baumdiagramm)
Stochastik
Etwa 60 Minuten: ein Tisch-Versuch zur bedingten Wahrscheinlichkeit und einer Auswertung über ein zweistufiges Baumdiagramm. Hier steht eine Schritt-für-Schritt Anleitung dazu. => Ganzen Artikel lesen …
=> Ganzen Artikel lesen …
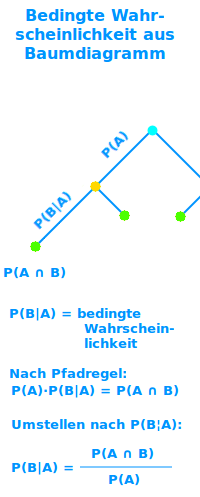Bedingte Wahrscheinlichkeit aus Baumdiagramm
Stochastik
Für zweistufige Zufallsversuche kann man aus einem Baumdiagramm immer bedingte Wahrscheinlichkeiten berechnen. Das ist hier erklärt. => Ganzen Artikel lesen …
Anleitung
Aus einem Baumdiagramm kann man in der Stochastik oft leich einen Erwartungswert berechnen. Das ist hier Schritt-für-Schritt erklärt. => Ganzen Artikel lesen …
… das kleine griechische Siehe unter => Erwartungswert über Baumdiagramm
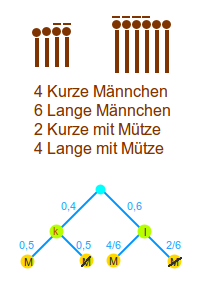Statistische Abhängigkeit über Baumdiagramm
Bestimmung
Hat man ein Baumdiagramm mit relativen Häufigkeiten zu zwei Merkmalen, dann kann man leicht erkennen, ob die zwei Merkmale voneinander statistisch unabhängig sind: ganz unten im Baumdiagramm gibt es von links nach rechts gehend vier Zahlen an den Ausgängen, die sogenannten Ausgangswahrscheinlichkeiten. Wenn die 1. und die 3. Ausgangswahrscheinlichkeit gleich sind und gleichzeitig auch die 2. und die 4. Ausgangswahrscheinlichkeit gleich sind, dann sind die zwei betrachteten Merkmale zueinander unabhängig. Das ist hier ausführlich erklärt. => Ganzen Artikel lesen …
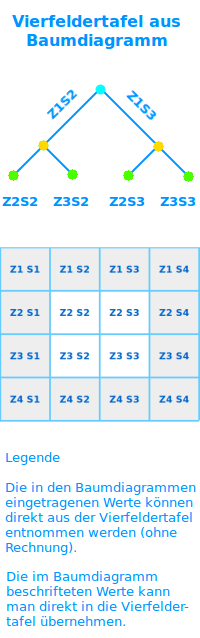Vierfeldertafel aus Baumdiagramm
Schema für die Umwandlung
Man hat ein Baumdiagramm, zum Beispiel für eine Statistik oder einen Zufallsversuch gegeben. Daraus kann man dann immer auch eine Vierfeldertafel (VFT) erstellen. Das ist hier hier kurz skizziert. => Ganzen Artikel lesen …
… siehe unter => Baumdiagramm aus Vierfeldertafel
Stochastik
Wie groß ist die Wahrscheinlichkeit, beim zweimaligen Würfeln genau zwei Vierer zu bekommen? Hier steht der Rechenweg mit einem Baumdiagramm kurz in Worten beschrieben. => Ganzen Artikel lesen …
Zweistufiges Baumdiagramm
… hat zwei Ebenen, modelliert => zweistufiger Zufallsversuch
